Please note, this week’s blog will be a little more context heavy as I work to establish the building blocks of a model I hope to add onto each week going forward.
This week, I implement new methodologies for more complex election forecasts. I examine model documentation of experienced forecasters, explore the impact of weekly polling data on election outcomes, apply new regression techniques to polls as predictors, and integrate economic fundamentals into a combined model as the basis of my future forecast.
Current Forecasting Methodologies
Many forecasters’ current models blend polling data with economic fundamentals. Reviewing advanced breakdowns from G Elliot Morris of 538 and Nate Silver of the Silver Bulletin, I note potential methods that I have implemented or could adopt.
Morris’s FiveThirtyEight forecast model for the 2024 election polling averages and state correlations through geometric decay, emphasizing state similarities in voting behavior, geography and demographics as correlates. The model combines this with economic fundamentals such as employment and consumer sentiment. This combination of fundamentals and polling, with some weighting scheme within and between the two, is implemented later. FiveThirtyEight’s use of Bayesian regularized regression to manage polling biases and Markov chain Monte Carlo to simulate electoral scenarios are another future area of work in my model.
In contrast, Nate Silver’s 2020 (FiveThirtyEight) and 2024 (Silver Bulletin) models adopt a more dynamic framework that adjusts for contemporary uncertainties, particularly changes in voter turnout patterns. Silver was not a fan of Morris’s model at The Economists, and criticized the new FiveThirtyEight model predicting a Biden win post-debate despite polling favoring Trump. Silver’s approach combines polling with economic conditions, incumbency, and demographic trends like shifts in voter turnout (more engaged Democrats). The model simulates thousands of election scenarios, giving more weight to polling closer to Election Day rather than fundamentals. Recent changes maintain the model’s core methodology while improving accuracy based on recent voting patterns.
Through these examples, my goal is to achieve a model that effectively combines polling data, incumbency, and economic fundamentals, utilizing Bayesian models, weighting schemes, and simulations.
Recent Polling Trends and the Use of Polling in Models
Polling– originating from Francis Galton’s 1907 Vox populi on the reliability of popular judgement– aims to gauge public sentiment but faces challenges in predicting crystallized outcomes. Thousands of polls are conducted to understand the race at a given time. But with so many complications in measuring the behavior of voters, it is extremely difficult for a poll to get the “right” answer.
These difficulties of polling are highlighted in Gelman and King’s “Why are american presidential election campaign polls so variable when votes are so predictable?” Variability in polls, as discussed in the analysis, shows that while polls fluctuate due to unforseen events, overall outcomes remain largely predictable based on fundamental factors. While voters may appear to change their minds during the campaign, they often make final decisions based on rational, long-standing preferences. Temporary polling swings often don’t reflect lasting changes in voter intentions.
For an example of this, look at variations in the 2020 election polling, with “game-changers” indicating significant events that may have influenced polling averages temporarily.
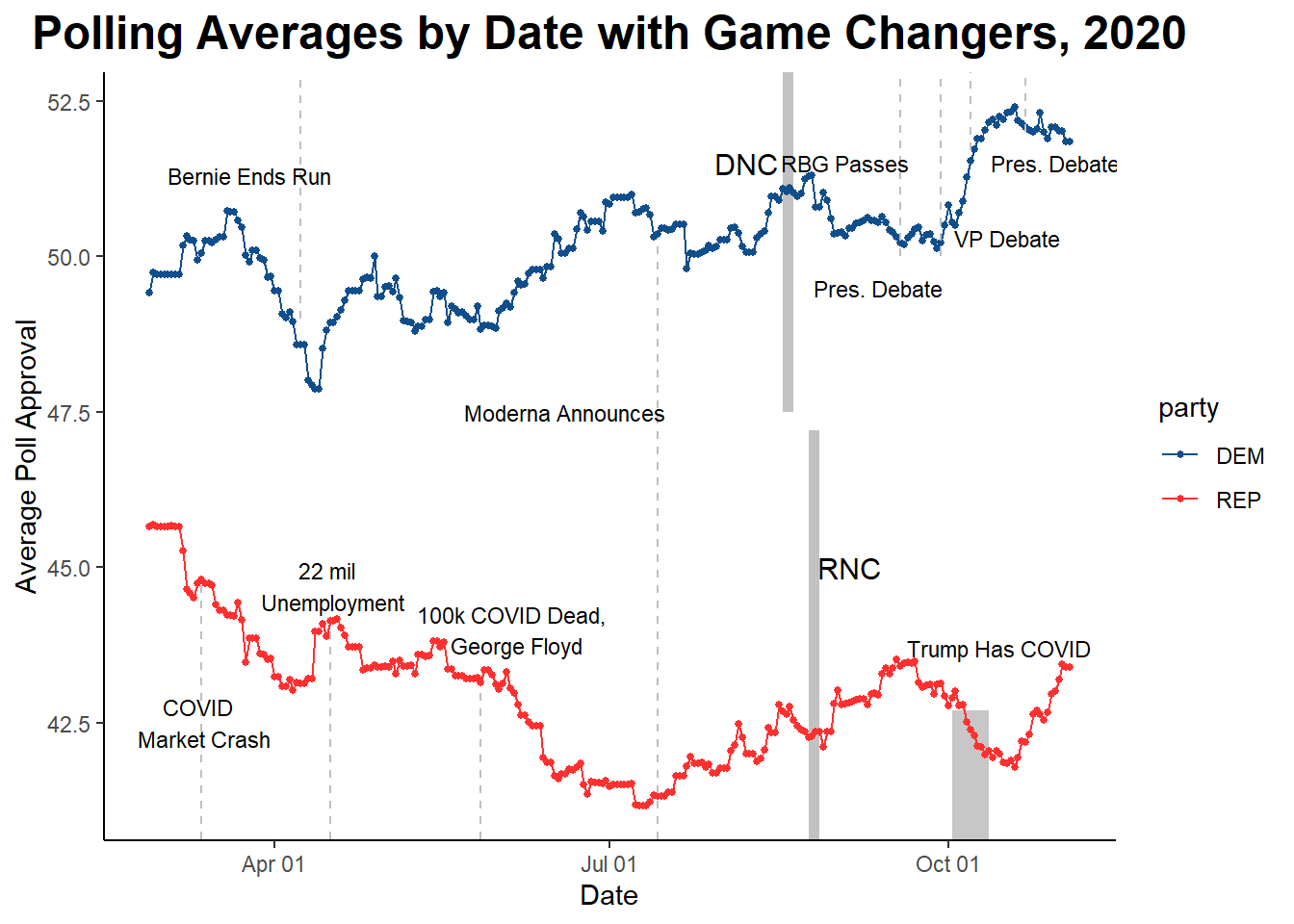
The variation in polls compared to the final outcome as described by Gelman and King is clearly seen here. For 2024 below, there is also a large amount of uncertainty, making modeling with weekly polling averages require advanced coefficient weighting.
Whether Biden’s polling data can be used without adjustment as a proxy for Harris like here is an open question I will later seek to answer.
Pollster Quality Evaluation
Different pollster methodologies and decisions impact the accuracy of polls. To account for this, FiveThirtyEight creates pollster ratings called “pollscores” which account for bias and error, and also look at transparency and percent partisan work. Variation in pollster quality can provide valuable information about the quality of the polling data my model relies on.
| Metric | Mean | Lower_CI | Upper_CI |
|---|---|---|---|
| Bias PPM | -0.02 | -0.057 | 0.017 |
| Error PPM | 0.067 | 0.039 | 0.096 |
| Pollscore | 0.016 | -0.013 | 0.046 |
| Numeric Grade | 1.744/3 | 1.702/3 | 1.786/3 |
| Weighted Avg Transparency | 4.05/10 | 3.894/10 | 4.207/10 |
| Percent Partisan Work | 18.44% | 15.86% | 21.03% |
These summary statistics for pollster quality reveal the limits of polling data. The current number one ranked pollster (The New York Times/Siena College) has a pollscore of -1.5, the best possible, no partisan work, and 8.7/10 transparency score. It is worth noting that the Predictive Plus-Minus for pollster’s absolute error, or error_ppm, is calculated as \[predictive\ error = adjusted\ error * (n / (n + n_{shrinkage})) + (group\ error\ prior) * (n_{shrinkage} / (n + n_{shrinkage}))\] , and Predictive Plus-Minus for pollster bias, or bias_ppm, is calculated as \[predictive\ bias = adjusted\ bias * (n / (n + n_{shrinkage})) + (group\ error\ prior) * (n_{shrinkage} / (n + n_{shrinkage}))\] , per 538 methodology, where n is the time-weighted number of polls the pollster has released and n_shrinkage is an integer that represents the effective number of polls’ worth of weight to put on the prior.
Through these complicated formulas, it is clear that pollster ratings are not particularly inspiring in accuracy of their poll results, at least according to these ratings. It is worth noting that transparency, which is a part of 538’s model, is not necessarily a direct correlate with accuracy of results, though this is difficult to test on a poll by poll basis given the lack of true comparison values.
A Brief Note on Regression Methodologies
Following in class evaluation of Ridge, LASSO, and elastic net regressions using cross-validation to find the optimal lambda values that minimize the MSE of predictions in week-level training data, I have decided to focus on the elastic net regularization method for this week. I will also use model ensembles to combine fundamentals and polling data such that I can weigh the different elements’ impact by time until election.
Polling-Based Regression Models
In past weeks, we have seen how simple OLS models with economic fundamentals are better than random predictors of election outcomes as univariate regressions. Now, we will use an ensemble model to weigh the results from individual polls in 2016 and 2020 by recency to 2024 election, using 2024 data as a test set after each years’ elastic net regression model is created.
| Party | PV2P |
|---|---|
| Democratic | 50.16656% |
| Republican | 50.08655% |
Compared to the single polls-alone elastic net regression run in lab (Harris 51.79268% - Trump 50.65879%), these results are quite similar despite the very different weighting scheme with the ensemble of elastic net regressions. For more model specifications, see the GitHub code. This forecast can be improved upon by adding fundamentals, as below.
Combined Fundamentals and Polling Elastic Net Regression Model
A combined fundamentals and polling model may help get closer to the ground truth of how voters think. The trouble with this ensemble is determining what should matter more closer to election day: polls or fundamentals. I will compare two combined models to understand this decision. In the future, I will add in state-by-state results and incumbency.
| Party | Prediction |
|---|---|
| Polls More | |
| Democrat | 51.71210 |
| Republican | 50.22182 |
| Fundamentals More | |
| Democrat | 51.31497 |
| Republican | 50.00100 |
Like with the polling-only model, these show Harris slightly leading Trump, though by slim margins. Additionally, weighing polls or fundamentals more as November nears leads to the emphasized group having a weight nearly 85% of the ensemble model, a large influence that really only results in a 0.2 to 0.4 percentage point difference given the above. However, that could be the margin of victory. The similarities in prediction also indicate a variety of factors working together over one strongly correlated one. For now, my final prediction is the unweighted average of the three done here today
Current Forecast: Harris 51.0645% - Trump 50.1031%
Data Sources
- Pollster Aggregate Ratings
- 2016, 2020, and 2024 Polling Results
- Popular Vote by Candidate, 1948-2020