Note: For this week of class, I was in charge of putting together a presentation of my findings. As a result, this post and the accompanying code as seen on Github contain many more plots than in past weeks, many of which are simply descriptive and exploratory statistics.
Happy 30 days until the election all! This week, I focus on refining my models by introducing the final fundamentals I have learned in class, demographics and turnout data. Additionally, I hone in on the states identified last week through expert prediction to be those I will model exclusively as they are the swing states that could decided the next president of the United States. These states are Wisconsin, Pennsylvania, North Carolina, Nevada, Michigan, Georgia, and Arizona.
The decision to predict the popular vote in these states alone stems from the expert predictions from organizations like the Cook Political Report and Sabato’s Crystal Ball, who predict most other states to be safely in either Donald Trump’s or Kamala Harris’s court for the upcoming election. As such, I count their electoral vote for their respective candidate and move to predict the lesser known outcomes of the seven swing states.
In this blog post, I begin by exploring the voterfiles for these key states, diving into the specific demographics and those which are most associated with voting behavior. Additionally, I replicate Kim & Zilinsky (2023) findings on the power of demographics to predict turnout and voter share using ANES data, deciding if and how to incorporate this new data point into my model. Building on the elastic net regression ensemble of polling data and economic fundamentals from the last few posts, I explore simulations of the result of the election, also considering random forest methods.
Exploring the Voterfile
Voterfile data allow me to see granular information on the demographic characteristics of the voting population of each state. The voterfiles for this post were graciously provided by Statara Solutions. In the following plots, I break down the voterfile data for our seven states of interest
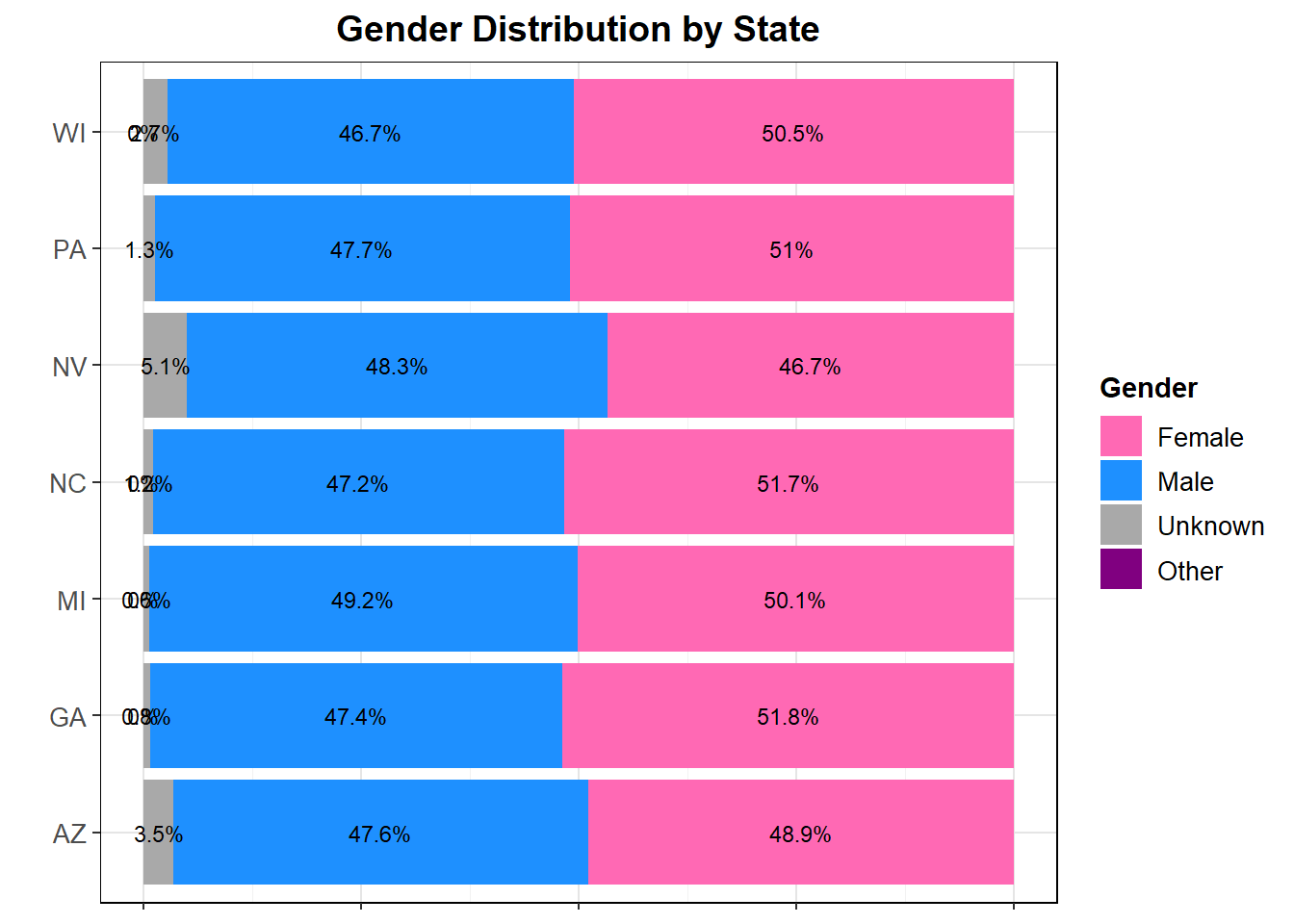
The gender splits of each state are not surprising, with most being around 50/50. While gender alone may not be able to provide significant and high percentage information on who someone is voting for or whether they turn out, what combined with other demographic variables it is possible it may be a statistically significant predictor, as I will explore below.
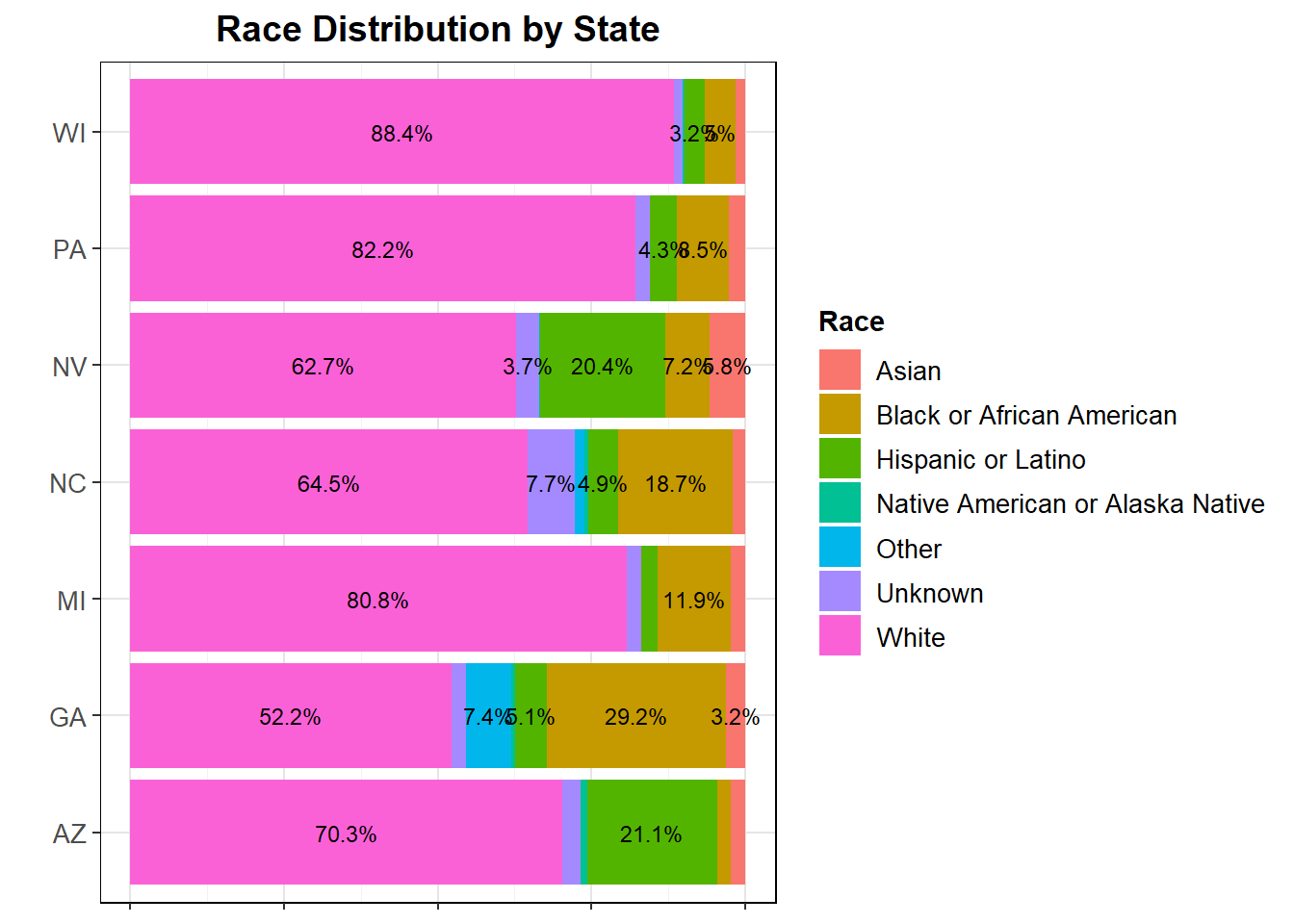
The distribution of race demographics in the states of interest is more varied than gender. As certain racial demographics may lead to certain political views, which I will attempt to explore later, these different makeups may lead to differing support for the two candidates in these states. The fact that the voters have different characteristics may make it likely that they may support different candidates. It is important also to note that while many states have a large number of white people on the voterfile, large groups of minorities like the hispanic popular of Arizona or African American population of Georgia are often cited on the news as important voting blocks to watch for. However, it is likely that these groups are not a monolith.
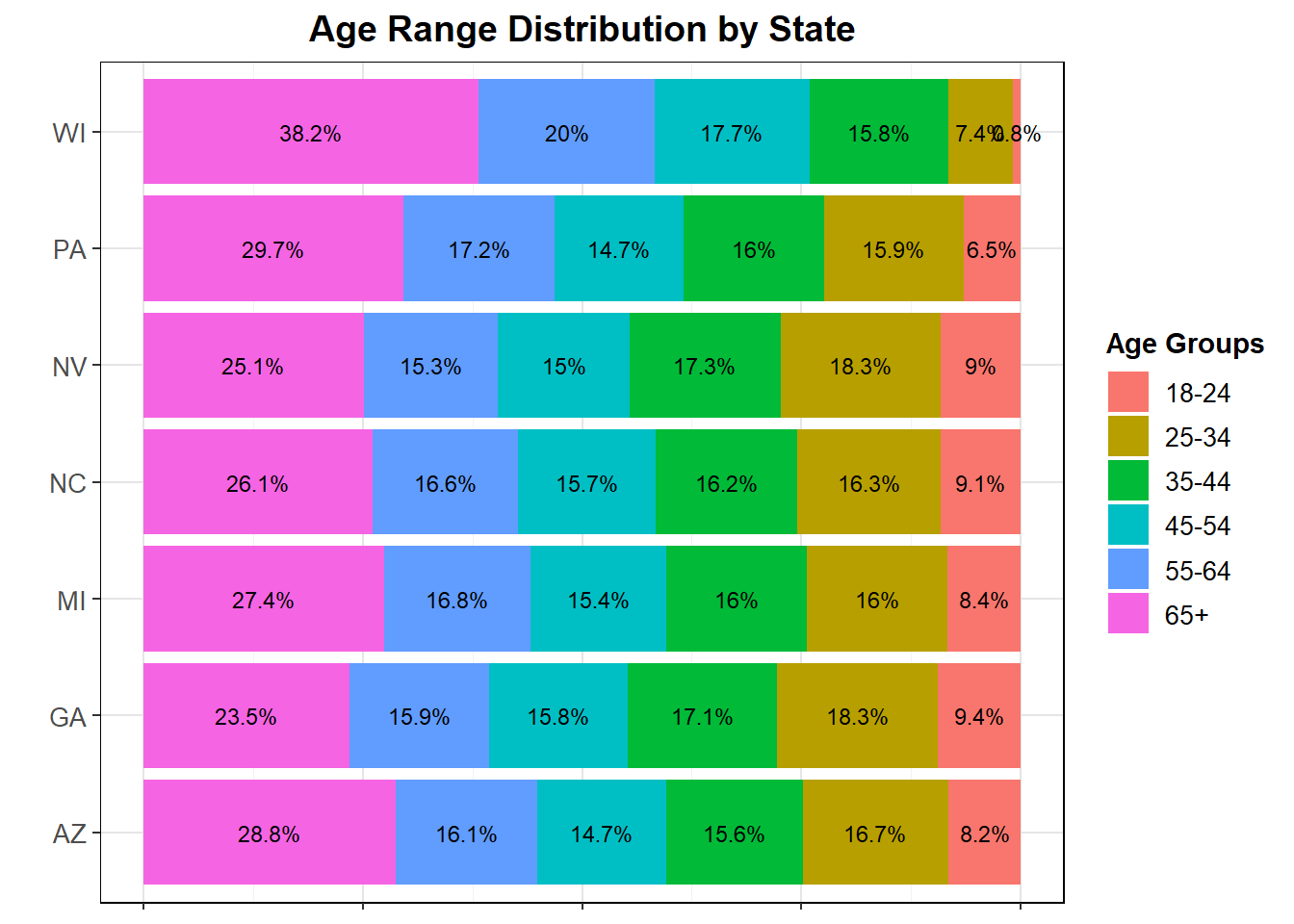
The variation in age may also effect turnout or popular vote outcomes, especially when combined with other demographic variables. Age is consistently found to be a good predictor of turnout in logit regressions of historical data, as in Matsusaka and Palida (1997). They also find education to be a good predictor. Looking later at Kim and Zilinsky (2023), I will explore how much of past turnout and popular vote outcomes these and other demographic variables can really explain.
While looking at demographics alone can tell me about the makeup of each state, it is also important to understand how each group acts. Below, I plot the percent of people in each age x race category that voted in the 2020 general election. For many groups, it surprisingly low, while for others there is incredibly high turnout (though these groups are consistently very small). The height of each bar represents the percentage of people in that age and race category who voted in the 2020 general election.
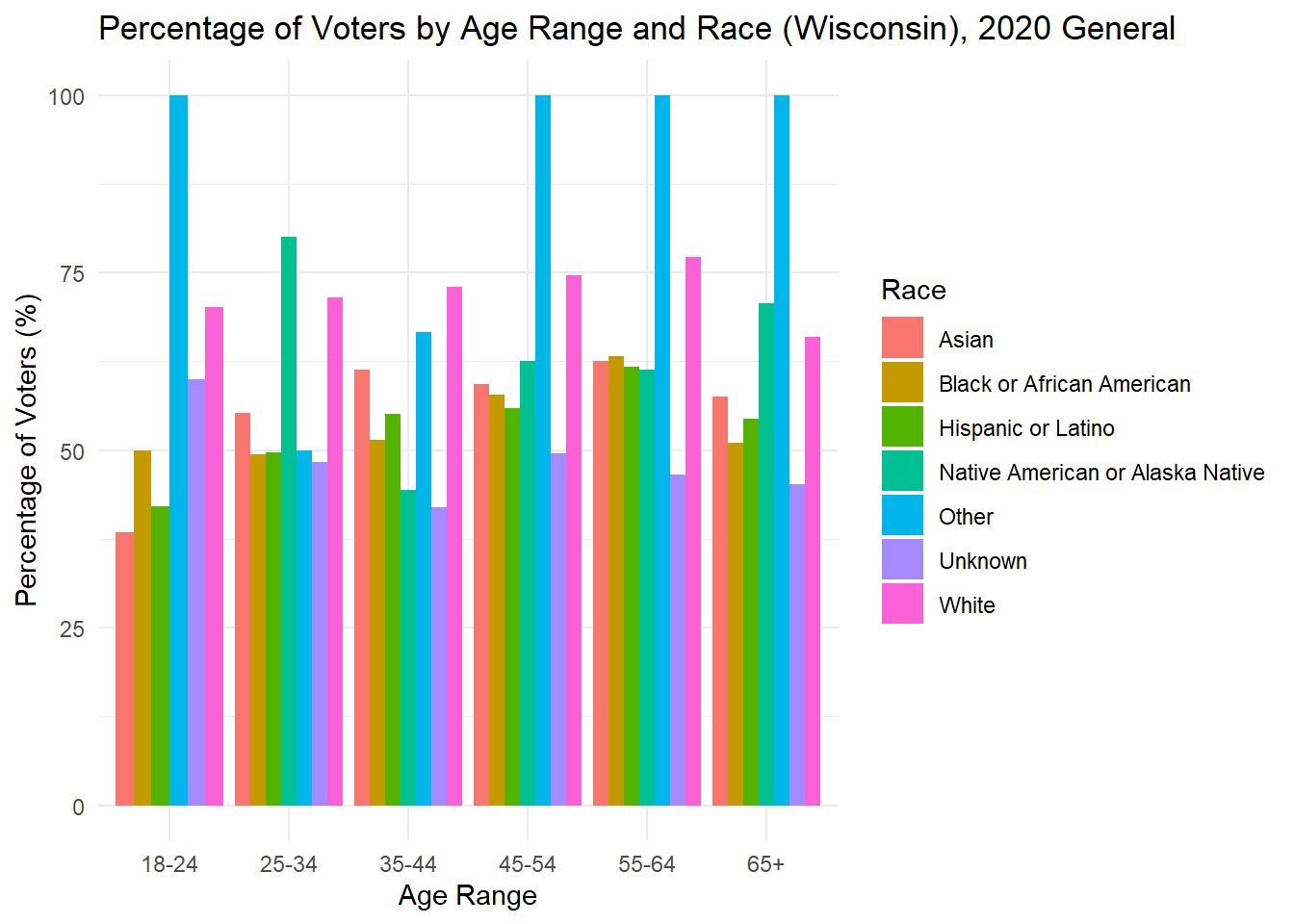
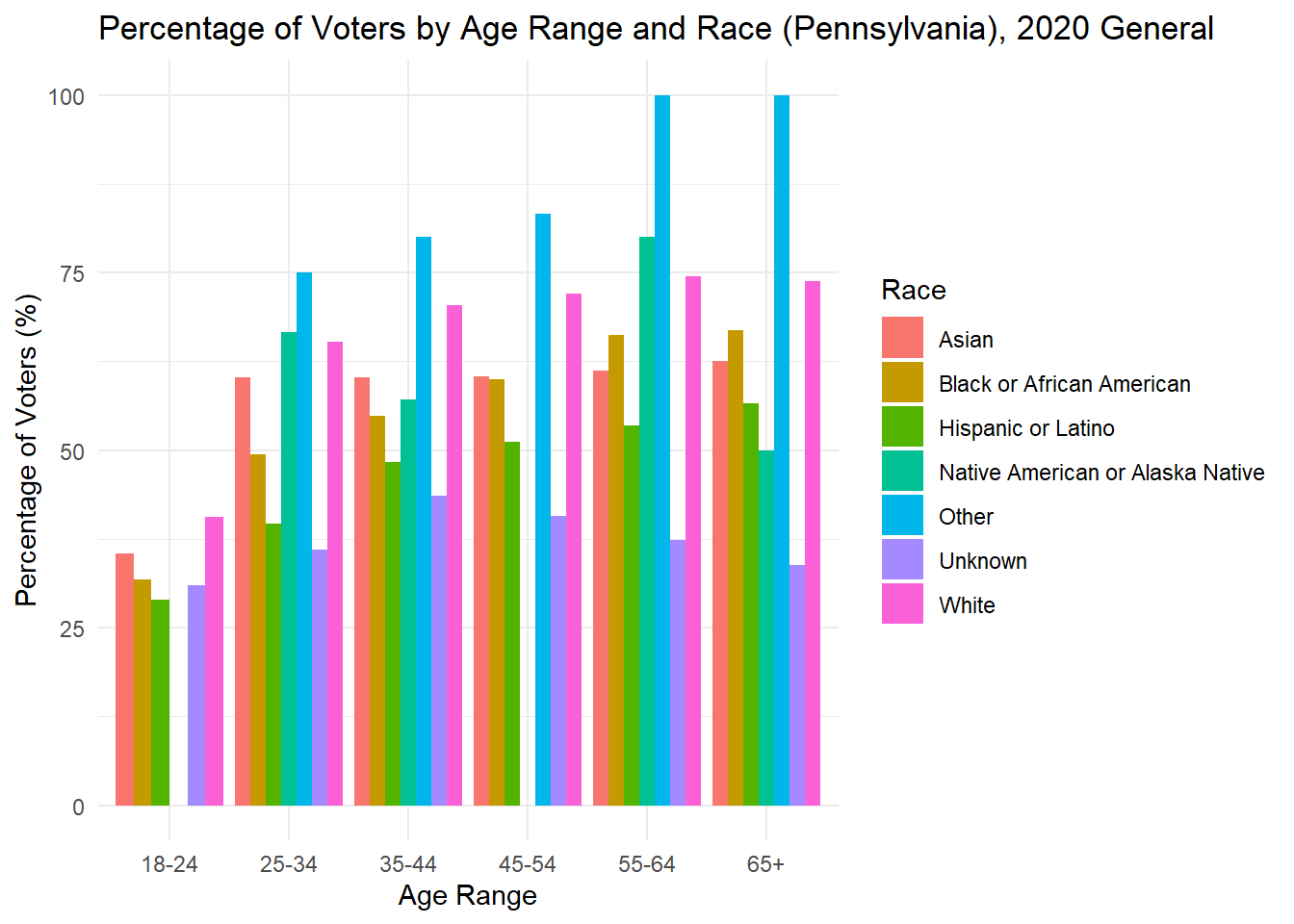
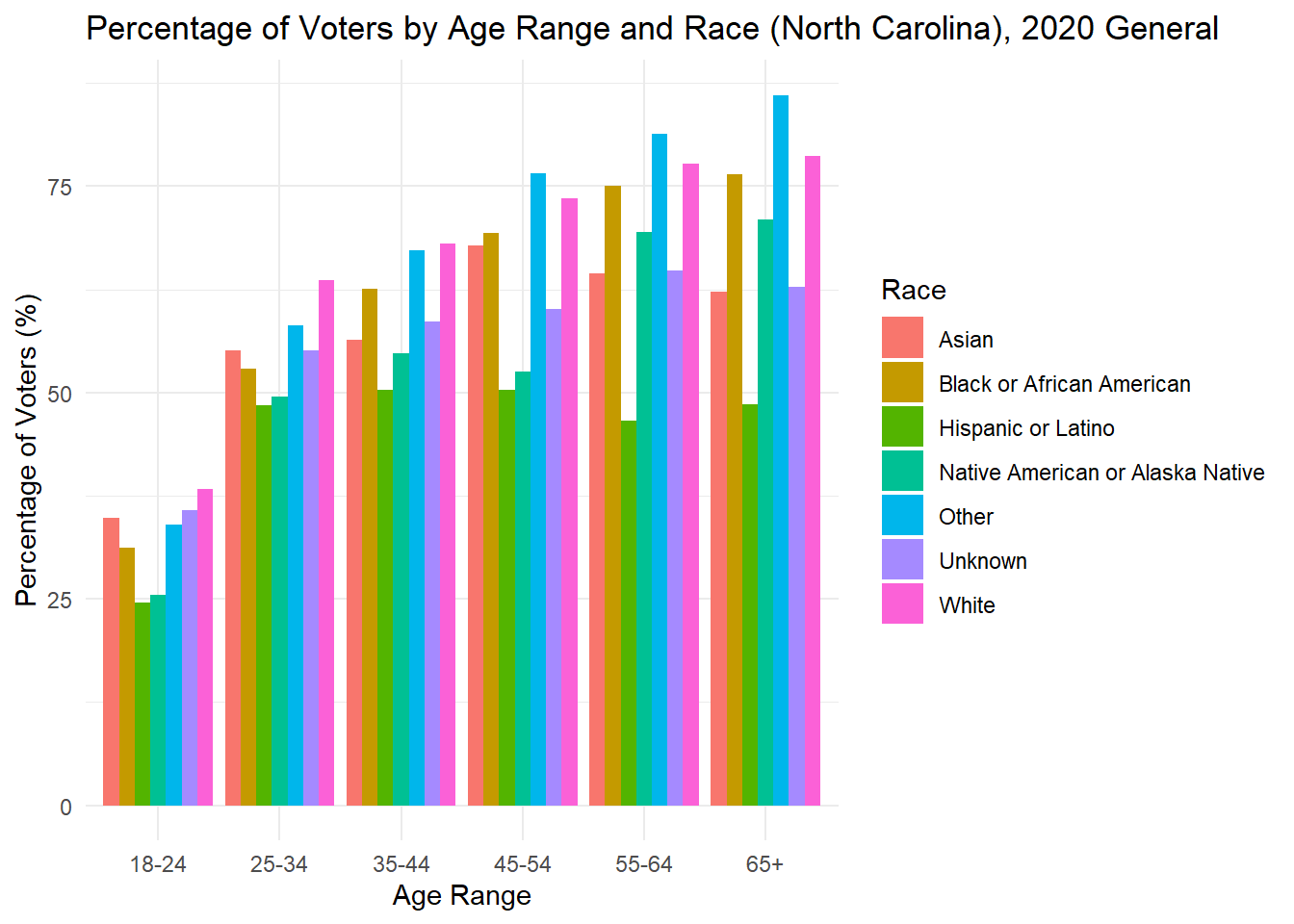
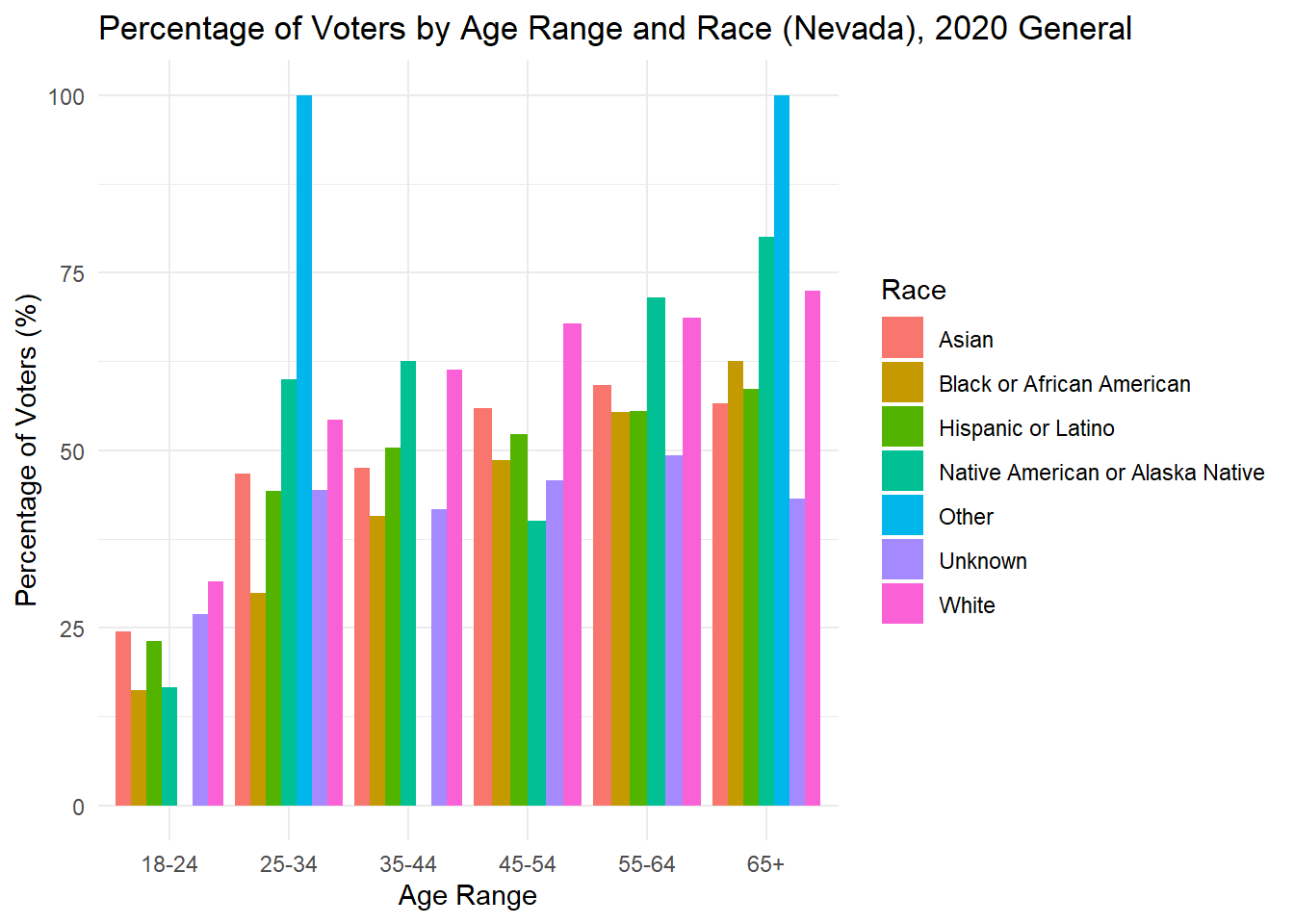
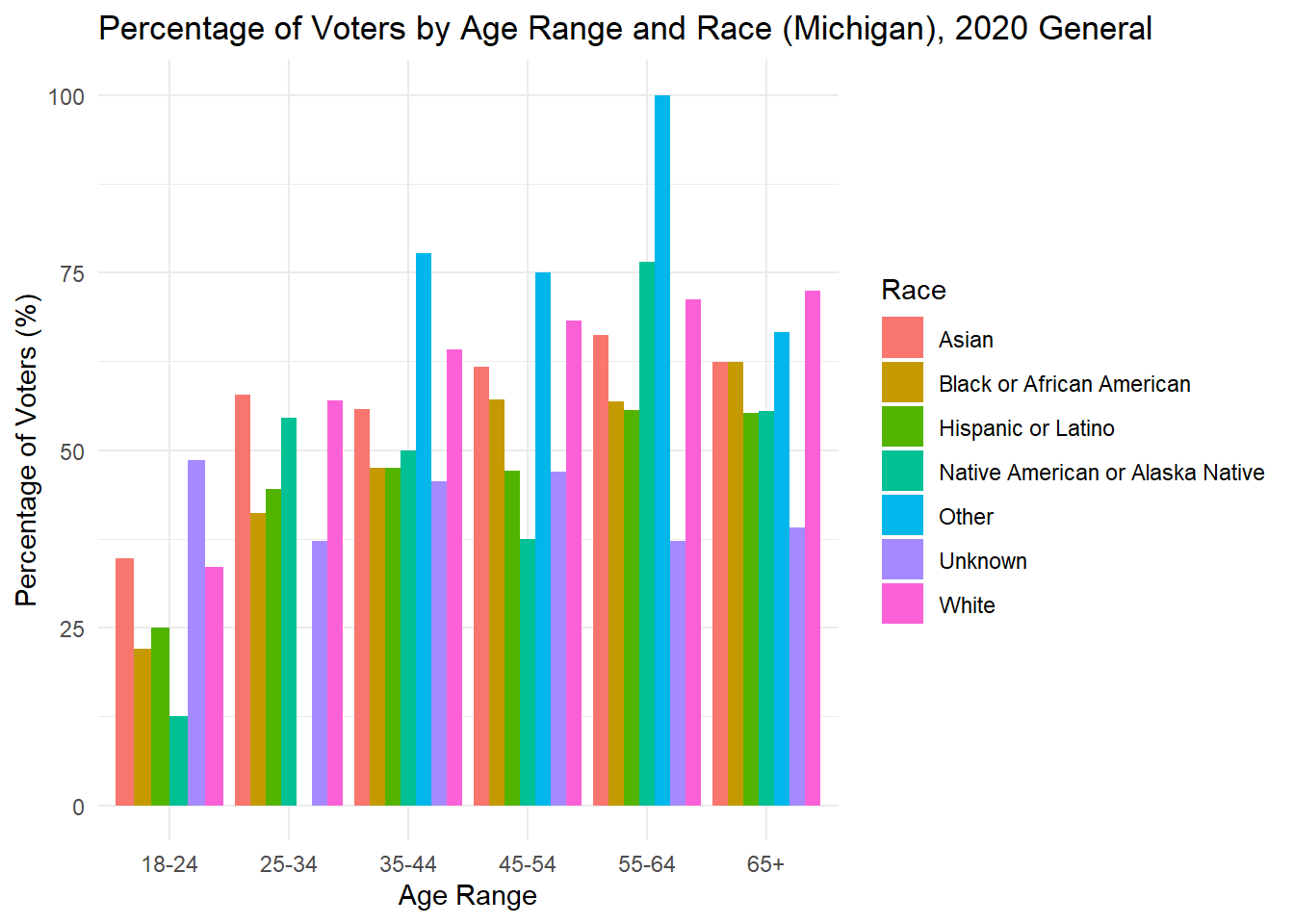
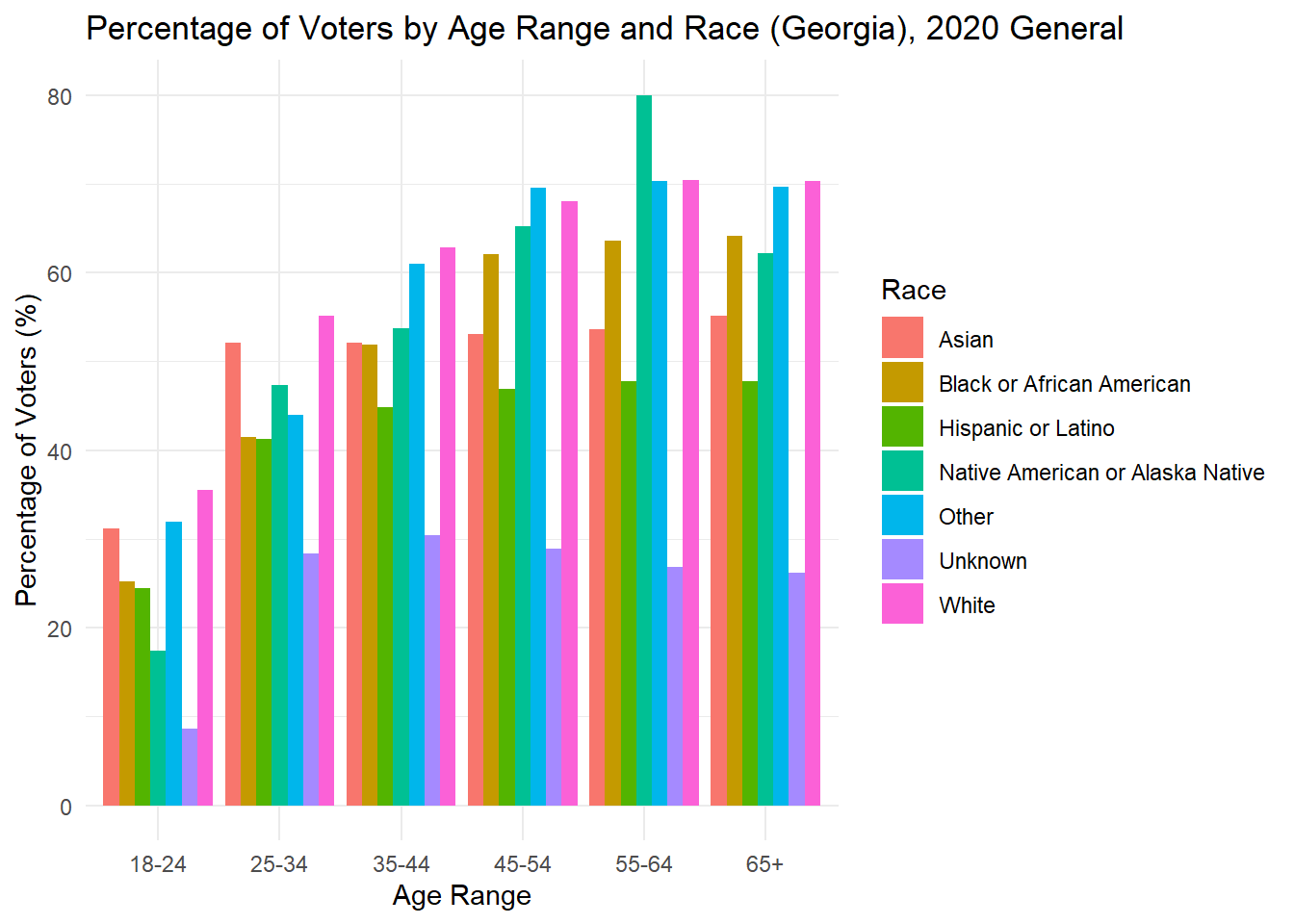
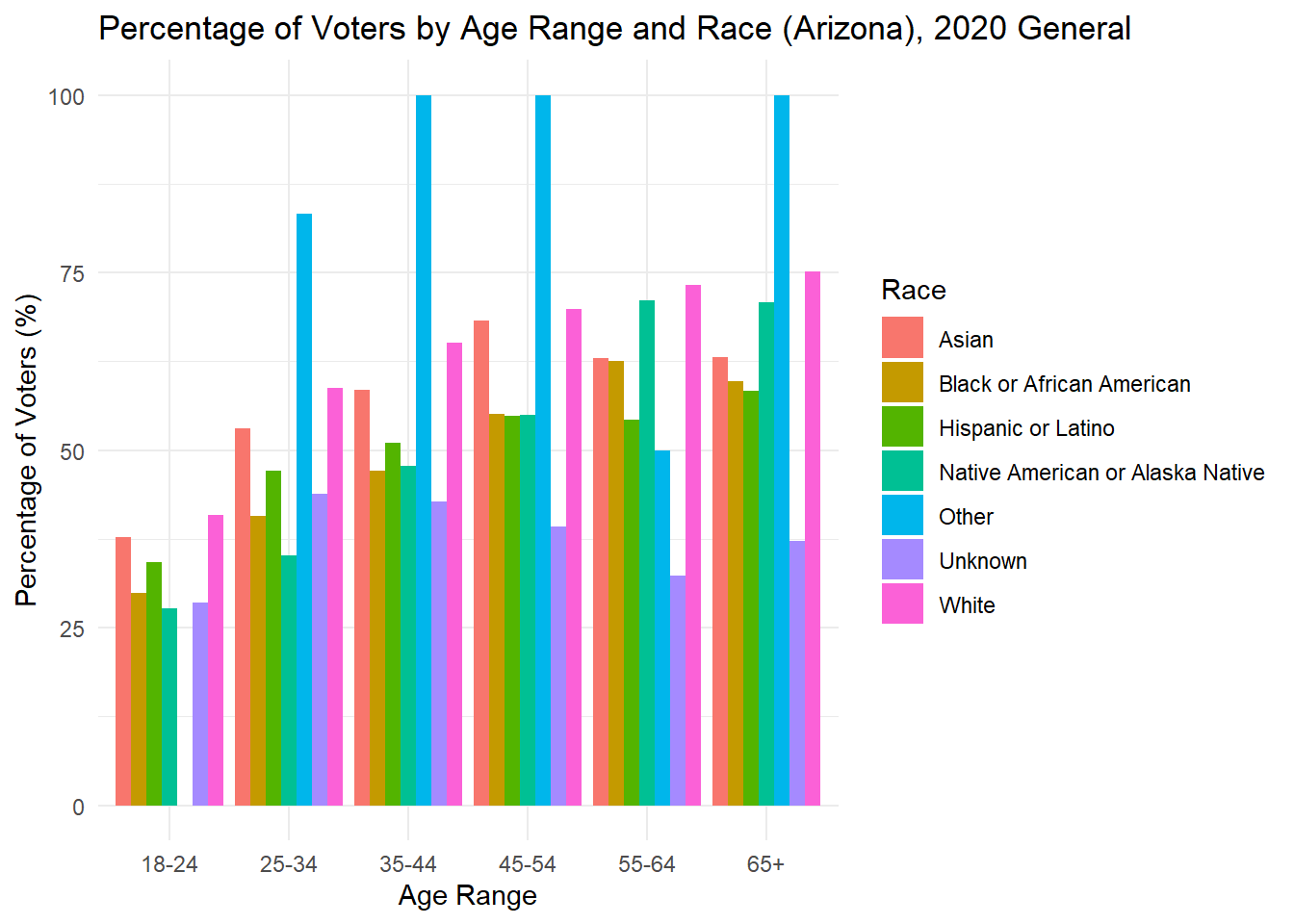
As is often observed in the literature, there is low turnout in 2020 among young people, but it is worth noting that 18 is the first year they can vote, and the ages in this data are up to date with 2024, making that group significantly smaller in the first place. To understand whether young people actually vote less, it would be best to dive into those currently aged 22-28 to see if and how they voted in 2020.
Below I also include these graphs as heat maps for ease of reading, but feel free to use whichever works best for your understanding.
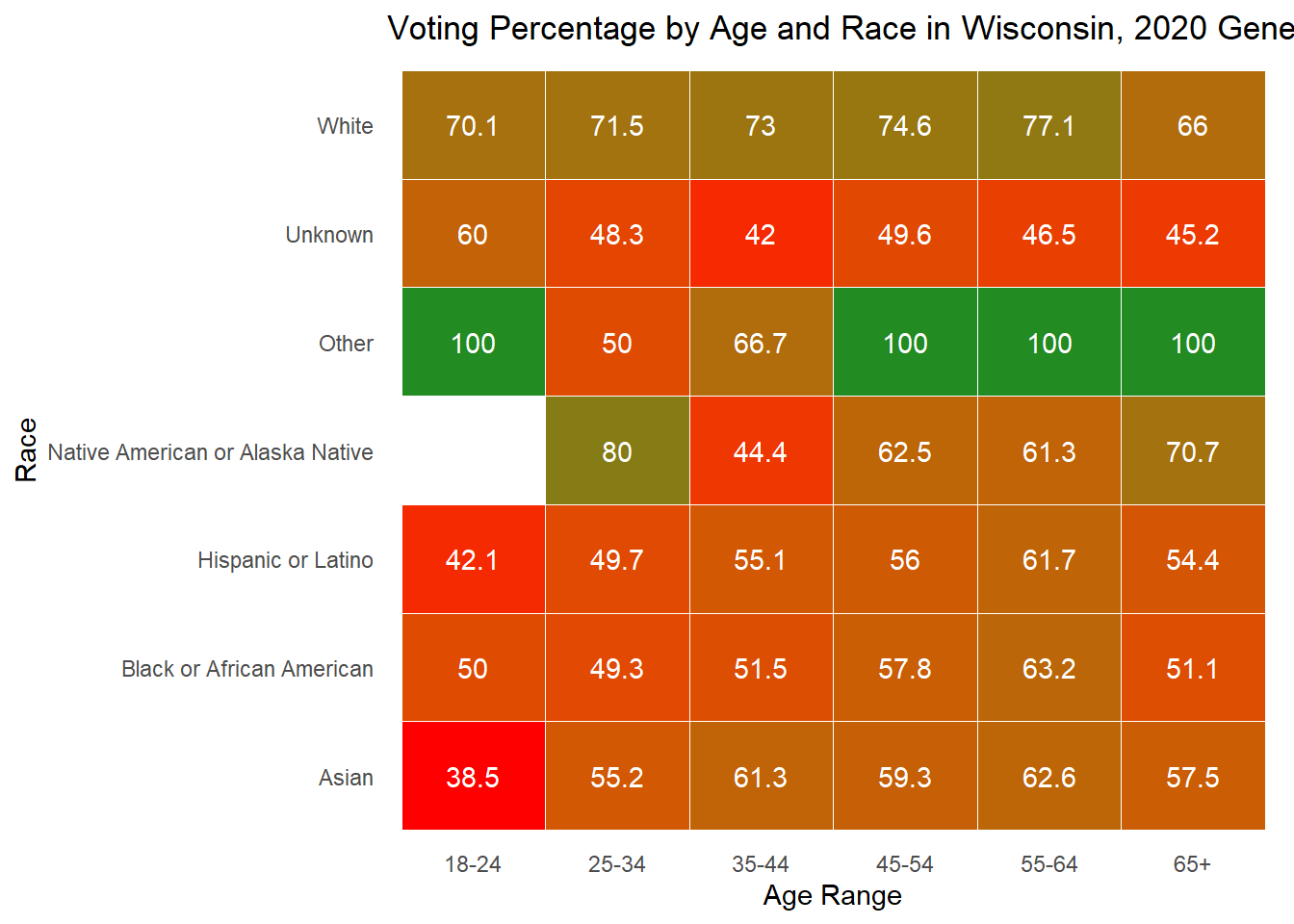
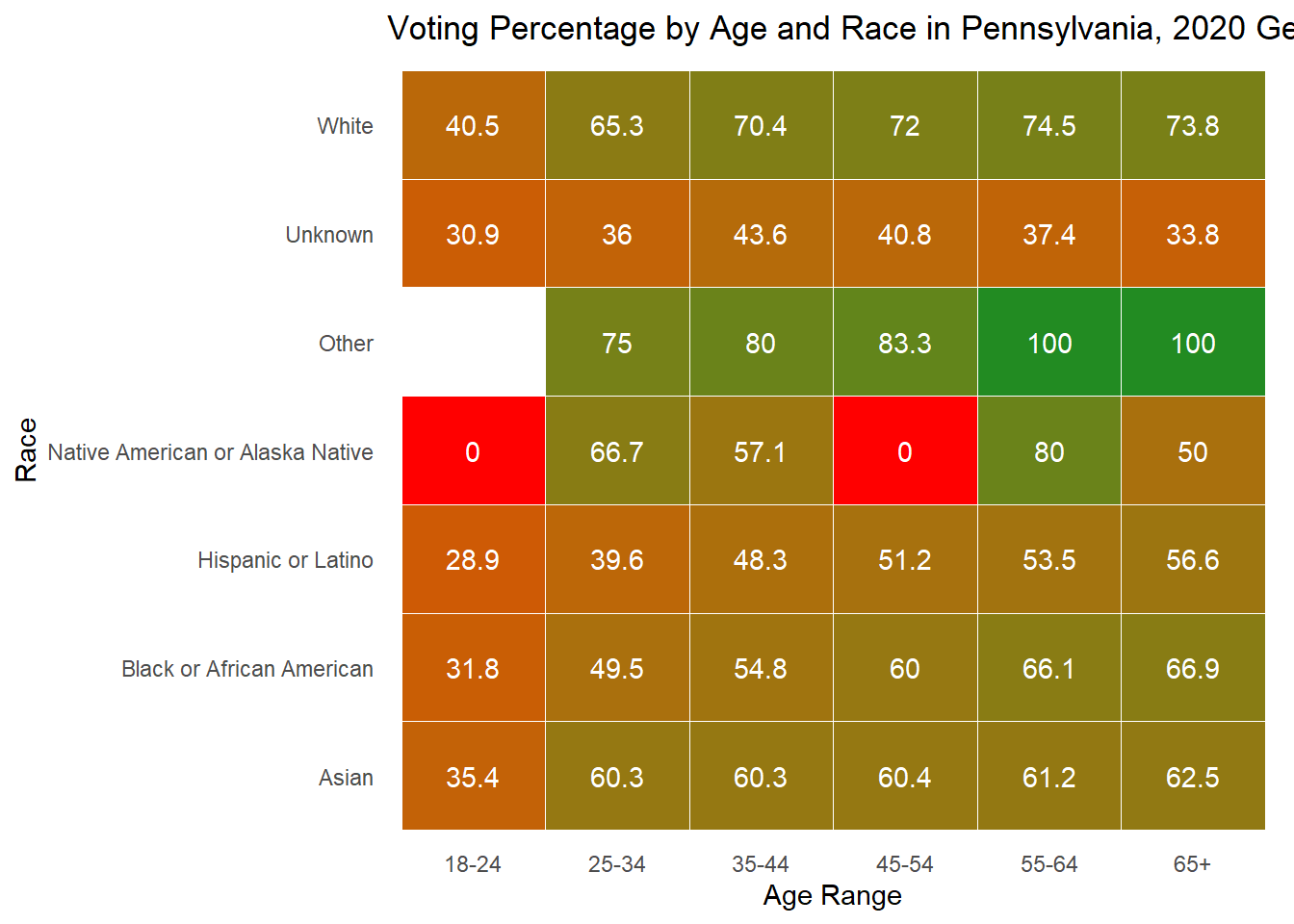
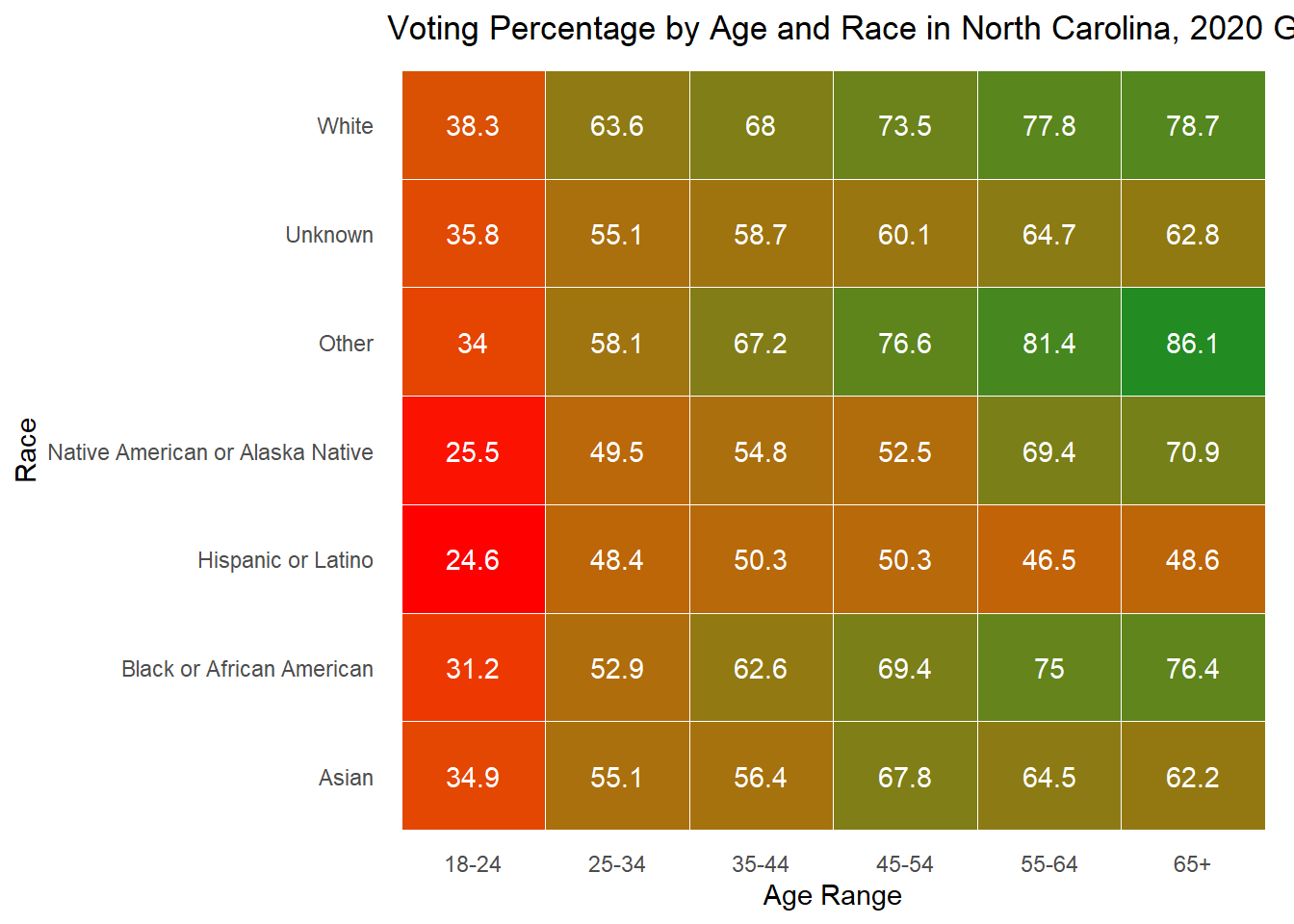
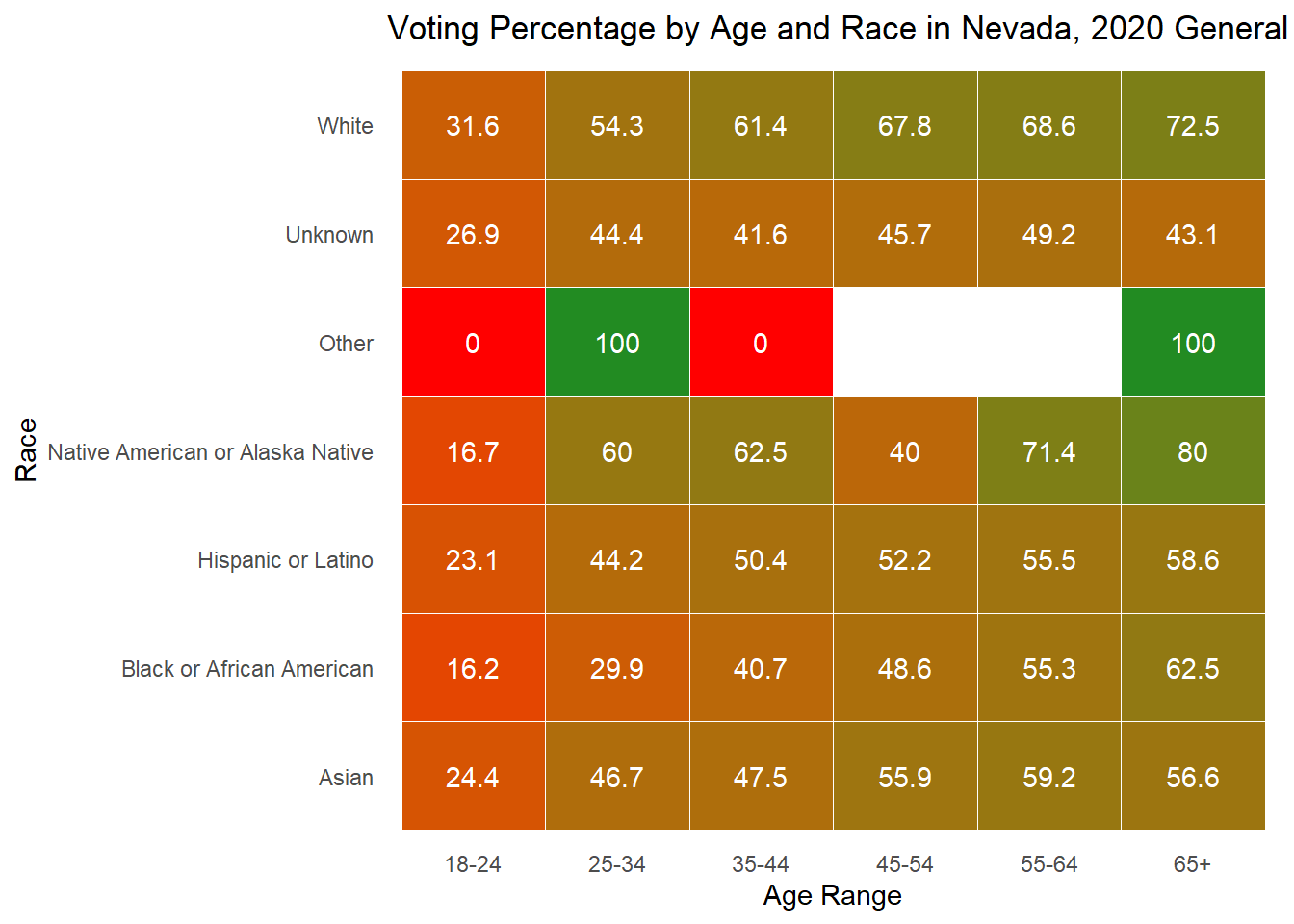
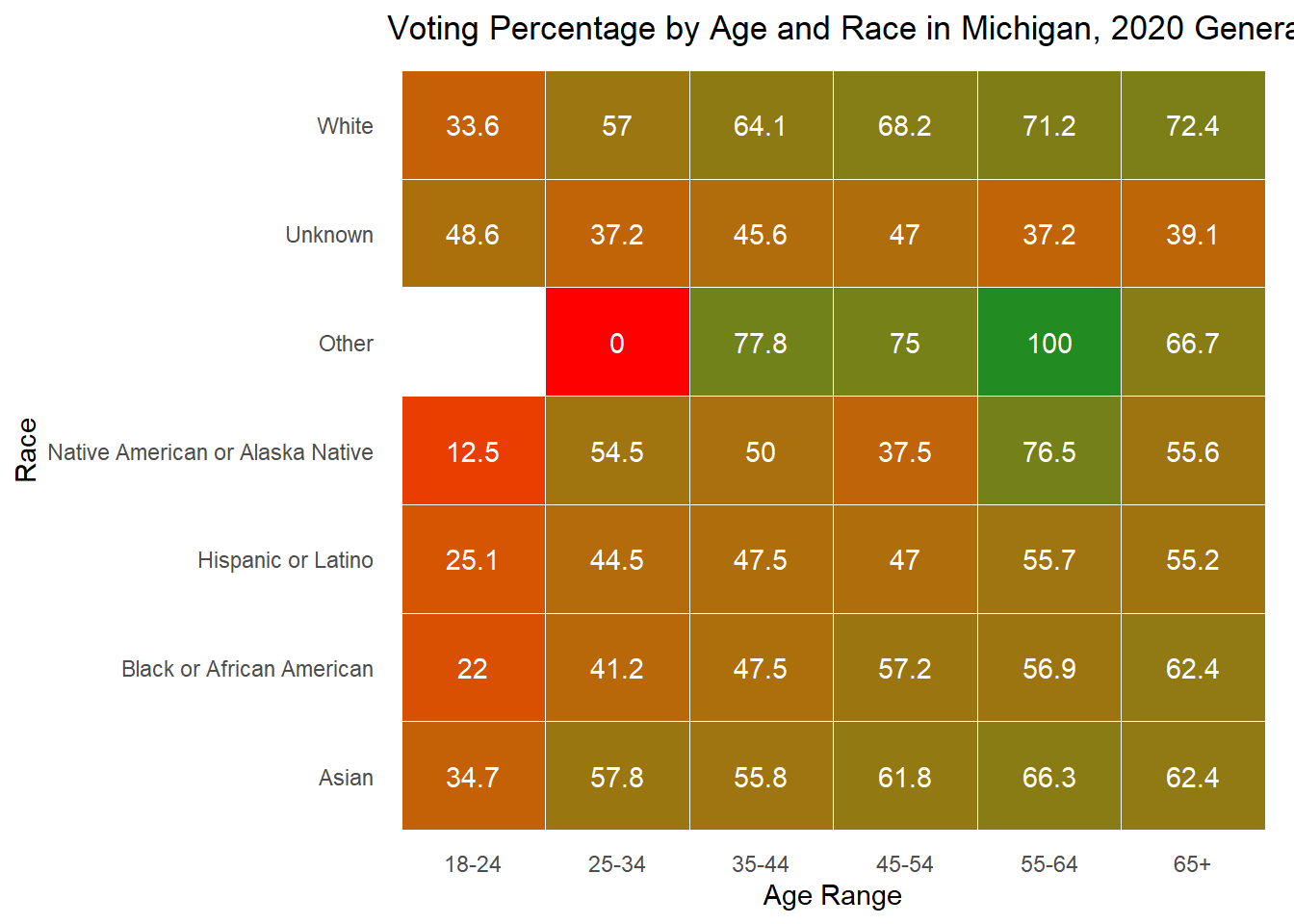
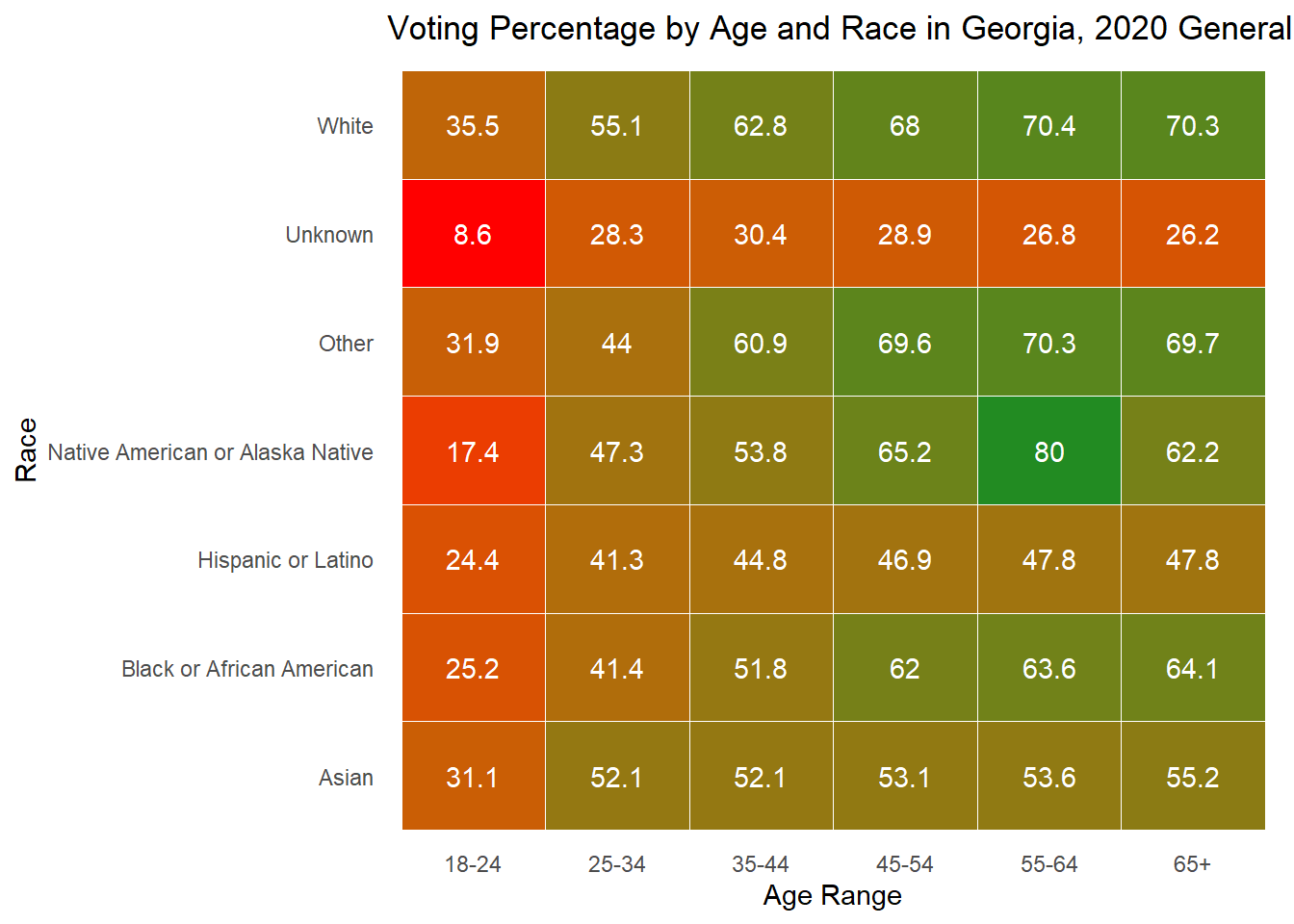
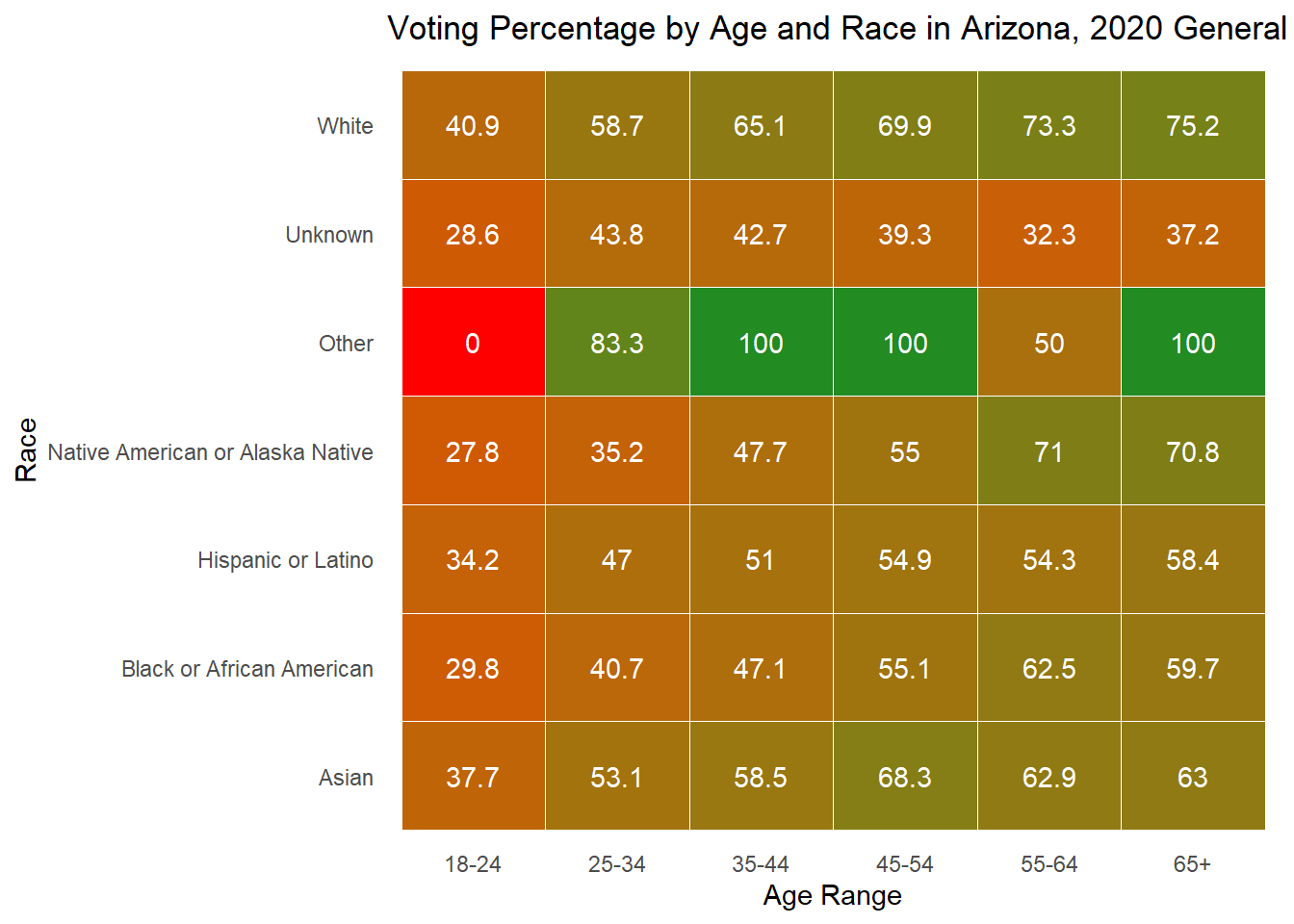
Overall, these demographic explorations provide the context necessary as I move into exploring whether they are good to include in my predictive model.
Demographics and Prediction
In Kim and Zilinsky (2023) on the predictive power of demographics on vote choice and party affiliation over time, they find that “models trained on nothing more than demographic labels from public opinion surveys (1952–2020) predict only 63.9% of two-party vote choices and 63.4% of partisan IDs correctly out-of-sample—whether they be based on logistic regressions or tree-based machine learning models.” While they admit that social sorting through demographics appears to have occurred, these trends do not allow the use of demographics to clearly predict someone’s voting decisions. Additionally, of the about fifteen demographic variables they test, they find that knowing the party id of a person is more predictive than these together. In this section, I replicate these findings and determine if demographic variables alone are a useful predictor to implement in my election prediction model.
The data from this analysis comes from the American National Election Studies (ANES), a long-running survey project that collects data on voter attitudes, behaviors, and demographics in the U.S., spanning every presidential election cycle since 1952. Unlike the U.S. Census, which focuses on counting the population and gathering general demographic information, ANES emphasizes understanding political opinions, electoral behavior, and voter psychology, offering insights into how and why people vote in particular ways.
To set up this replication, where my two outcome variables are partisanship and vote choice, I have chosen to use the features age, gender, race, income, education, urbanicity, region, southern, employment, religion, homeownership, and marriage, each split into indicator factors such that the specific values are tested for their importance. The two models I implement to test these factors and their accuracy are logistic regression and random forest models.
Beginning with the logistic regression’s ability to predict presidential vote choice, using 2016, below I train a model and then compare its in- and out-of-sample performance in the confusion matrices.
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | 4.3584*** | 0.4366803 | 9.9807136 | 0.0000000 |
| age | 7e-04 | 0.0028117 | 0.2483989 | 0.8038258 |
| gender | -0.4295*** | 0.0934585 | -4.5953379 | 0.0000043 |
| race | -0.5482*** | 0.0605982 | -9.0470969 | 0.0000000 |
| educ | -0.3398*** | 0.0613322 | -5.5405495 | 0.0000000 |
| income | 0.0494 | 0.0468039 | 1.0562135 | 0.2908707 |
| religion | -0.2148*** | 0.0421012 | -5.1023208 | 0.0000003 |
| attend_church | -0.211*** | 0.0331518 | -6.3644005 | 0.0000000 |
| southern | -0.4096*** | 0.1051603 | -3.8950560 | 0.0000982 |
| work_status | 0.0955* | 0.0458378 | 2.0838220 | 0.0371764 |
| homeowner | -0.1766* | 0.0822755 | -2.1458777 | 0.0318827 |
| married | -0.0716** | 0.0276917 | -2.5855402 | 0.0097227 |
| Democrat | Republican | |
|---|---|---|
| Democrat | 746 | 336 |
| Republican | 346 | 660 |
| Democrat | Republican | |
|---|---|---|
| Democrat | 184 | 80 |
| Republican | 88 | 169 |
The logistic regression is not separated by factors due to errors with the data, but the code for this can be seen in the Github and I will attempt to pursue it at a later date. The accuracy results of this regression mirror that of Kim and Zilinsky, with the demographic variables explaining 67.34% of in sample values and 67.75% out of sample. This can also be viewed in the attached confusion matrices. Of the variables (unfactored) that appear to have a statistically significant impact on vote share, the ones that are at the 5% level of significance include southern, religion, race, education, and gender.
I can also do a logistic regression for turnout, using NA values in the ANES presidential vote data as non-voters. Note again that this is for 2016, but could be done across years, as Kim and Zilinsky do for vote share and partisanship and get similar predictive power across all years, between 65-70%.
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | -1.6254*** | 0.3008608 | -5.4024799 | 0.0000001 |
| age | 0.017*** | 0.0020912 | 8.1265607 | 0.0000000 |
| gender | 0.1682* | 0.0720222 | 2.3347426 | 0.0195569 |
| race | -0.1016** | 0.0331625 | -3.0622153 | 0.0021971 |
| educ | 0.3856*** | 0.0460208 | 8.3788245 | 0.0000000 |
| income | 0.1478*** | 0.0341365 | 4.3287158 | 0.0000150 |
| religion | -0.1026** | 0.0313615 | -3.2726991 | 0.0010653 |
| attend_church | -0.032 | 0.0260078 | -1.2303698 | 0.2185587 |
| southern | 0.0469 | 0.0807981 | 0.5809961 | 0.5612431 |
| work_status | 0.0361 | 0.0343605 | 1.0518147 | 0.2928846 |
| homeowner | -0.0962. | 0.0513267 | -1.8736510 | 0.0609785 |
| married | -0.0248 | 0.0197024 | -1.2565859 | 0.2089036 |
| Did Not Vote | Voted | |
|---|---|---|
| Did Not Vote | 466 | 295 |
| Voted | 850 | 1805 |
| Did Not Vote | Voted | |
|---|---|---|
| Did Not Vote | 122 | 76 |
| Voted | 223 | 433 |
Slightly different than with vote share, it appears that the most statistically significant unfactored predictors of turnout are income, age, and education, which are consistent with the literature. As the confusion matrices show, the in-sample accuracy is 66.48% and out of sample accuracy is 64.99%.
I now transition to a random forest for presidential vote share and turnout, with similar set up to the logistic regressions above. The positive here is the democratic vote share, and I factored each variable such that individual levels can have an impact correctly due to the categorical nature of the data.
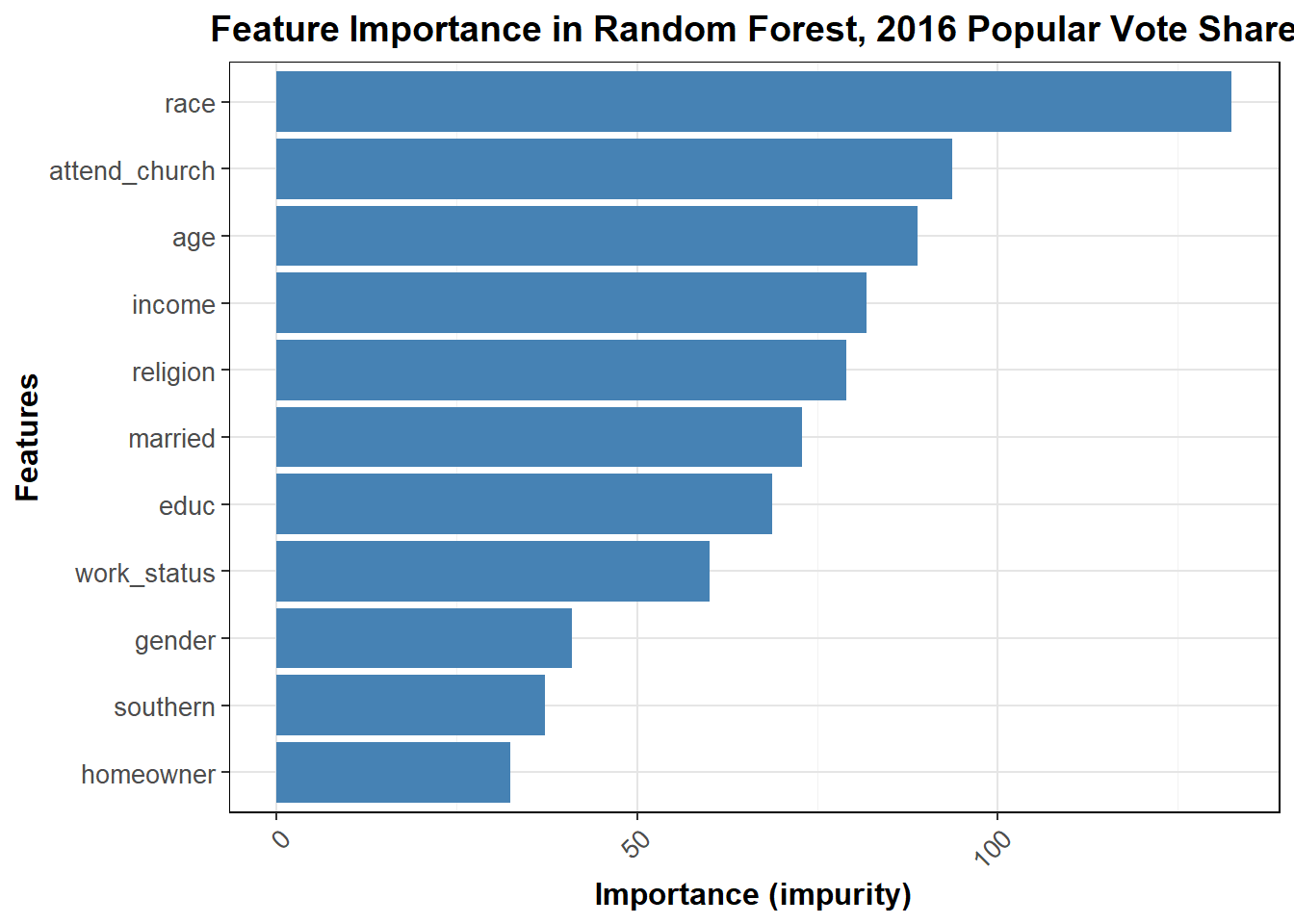In this random forest, I split the variables into their factors for proper analysis, leading to an in-sample accuracy of 71.65% and out-of-sample accuracy of 70.25%. The confusion matrices for these two cases are shown below.
| Democrat | Republican | |
|---|---|---|
| Democrat | 747 | 288 |
| Republican | 321 | 679 |
| Democrat | Republican | |
|---|---|---|
| Democrat | 193 | 73 |
| Republican | 74 | 168 |
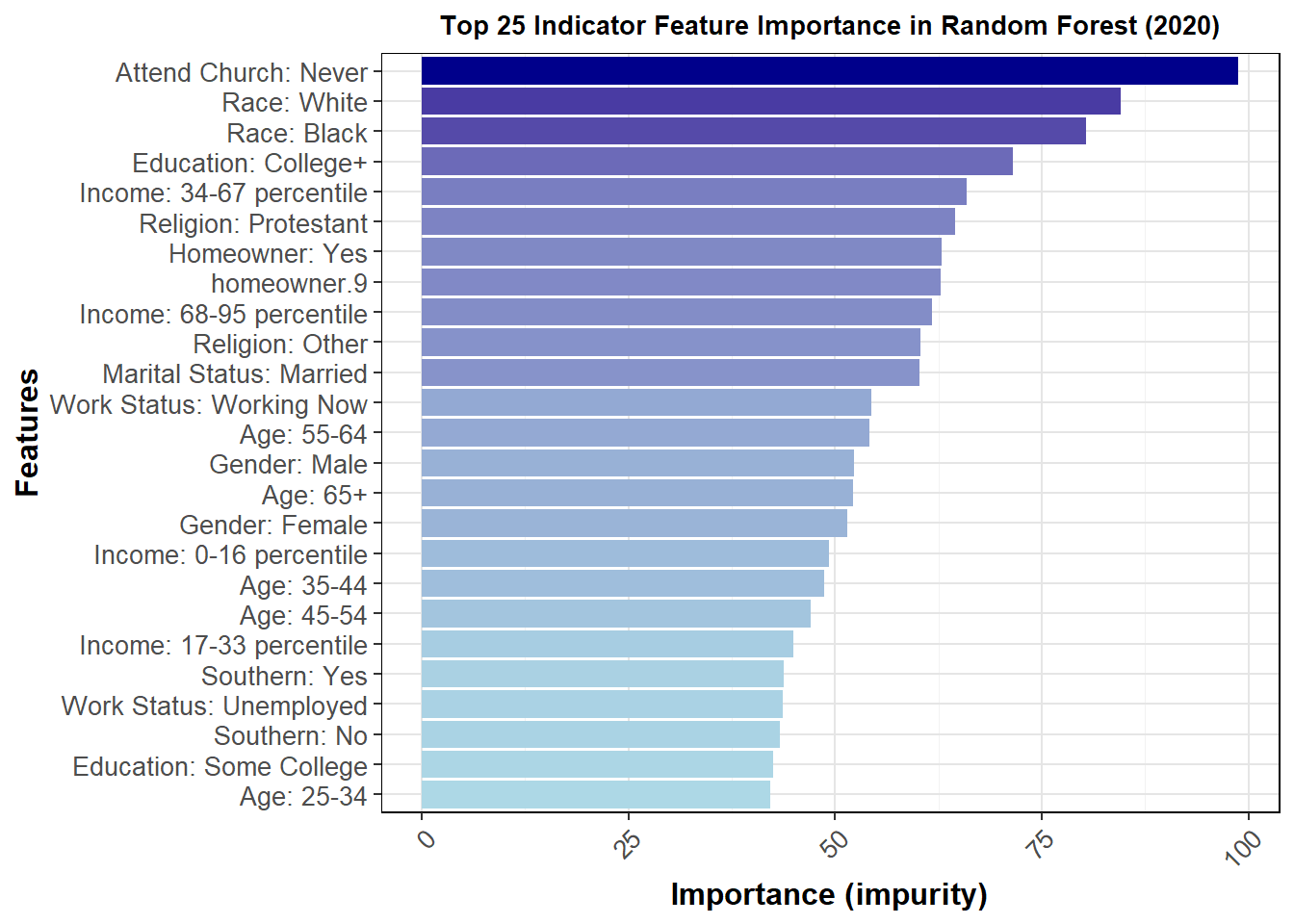
Based on the feature importance analysis (impurity) from the random forest model, age emerged as the most significant factor in predicting voting behavior, followed by race, church attendance, religion, and income. These features had a high influence on whether individuals voted Democrat or Republican, indicating that demographics and social factors played a crucial role in determining voter preference. Gender, southern residence, and homeowner status, while still contributing, had much lower importance values, suggesting that they were less impactful in the model’s overall predictions. The findings underscore the importance of understanding voter demographics and personal attributes in political analysis, but the accuracy from splitting the variables by factors was not greatly improved overall.
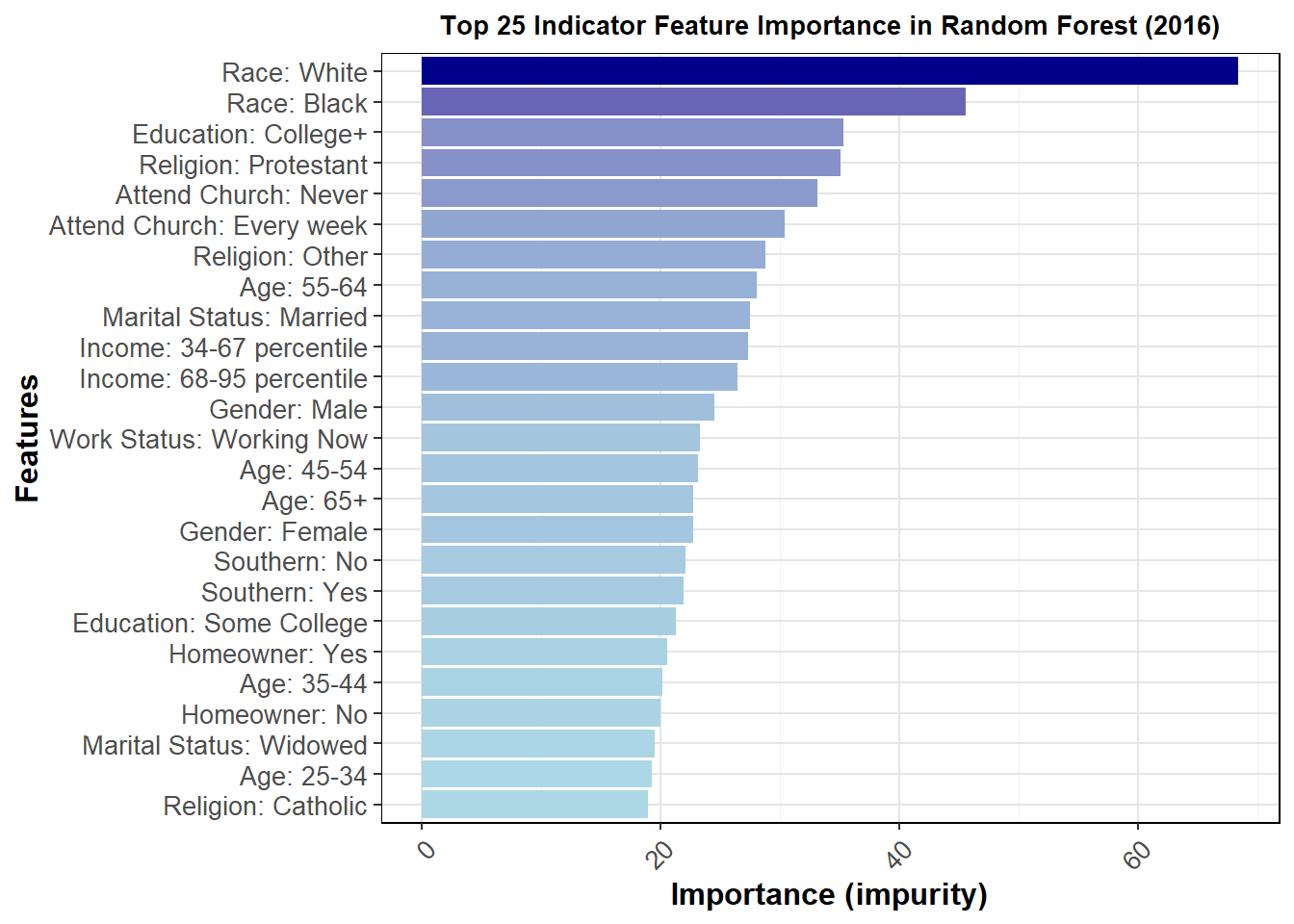
I can also perform one-hot encoding to view the individual contributions of the levels factored from each variable. A graph of the 25 most important factors but impurity is shown below.
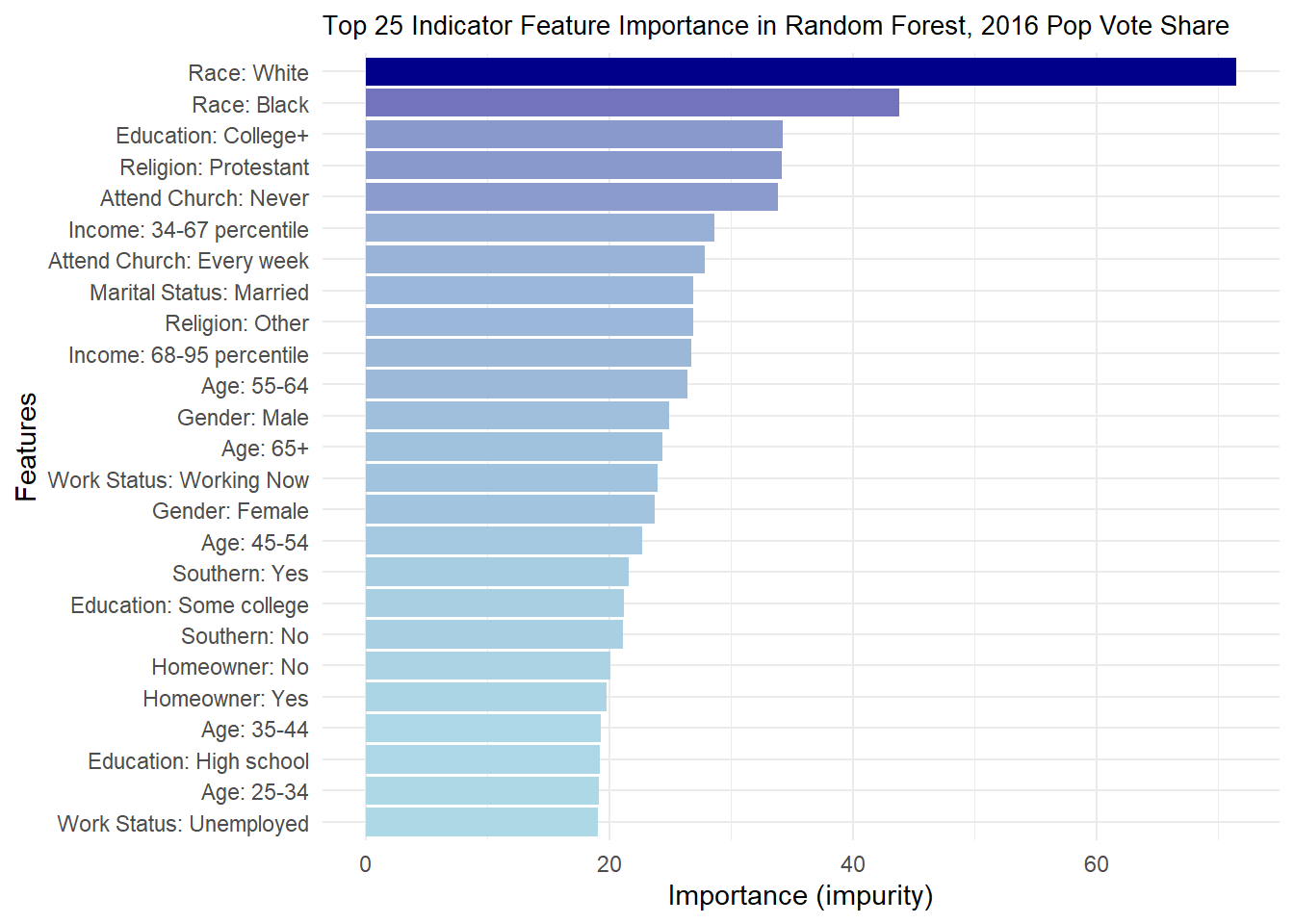
This graph gives us insight into which groups were most important at determining vote choice. The better a node is at splitting the data correctly, the more important it is, as measured by impurity. Because the above only looks at 2016, I thought it would also be important to see how much this changes for 2012 and 2020.
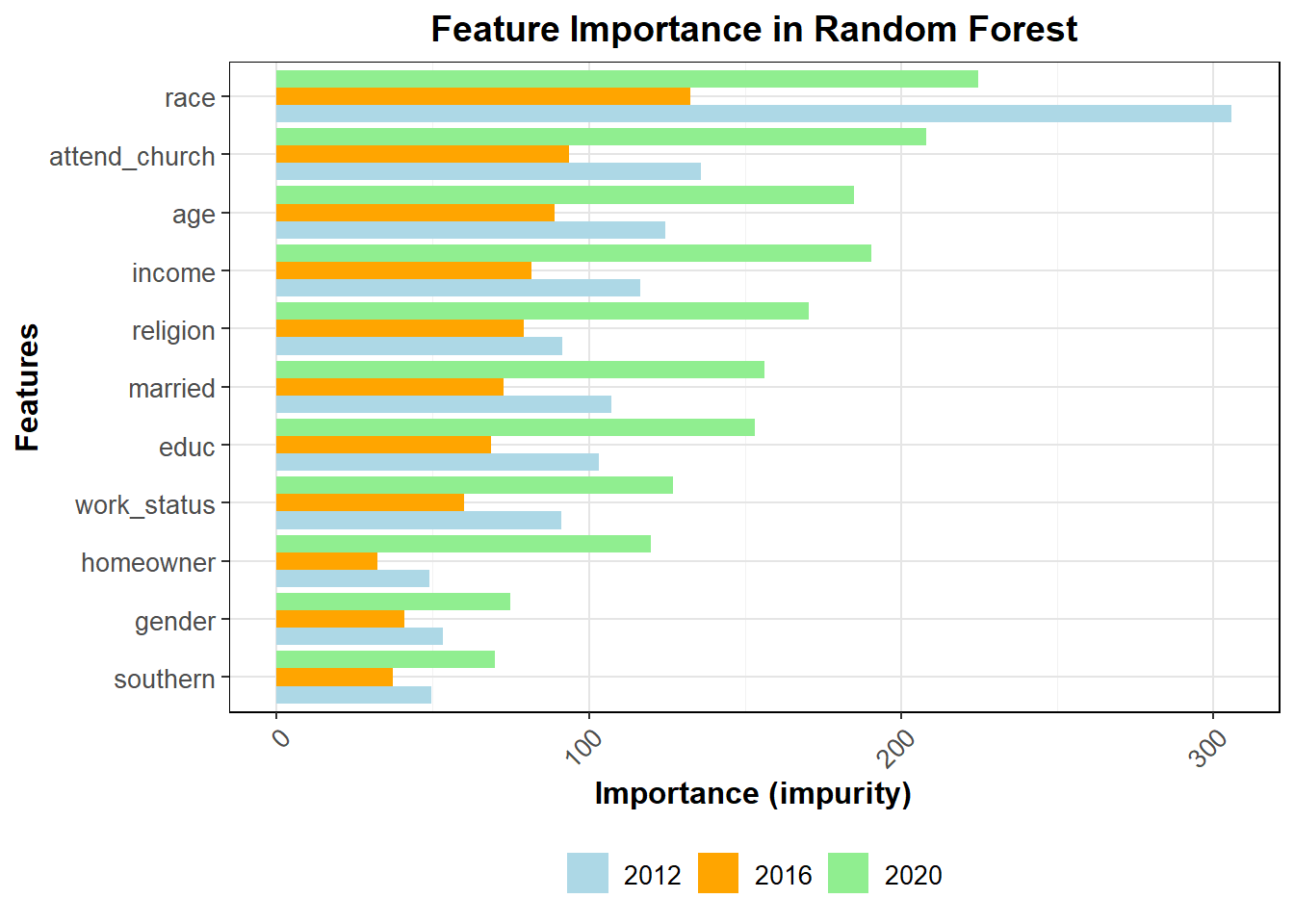
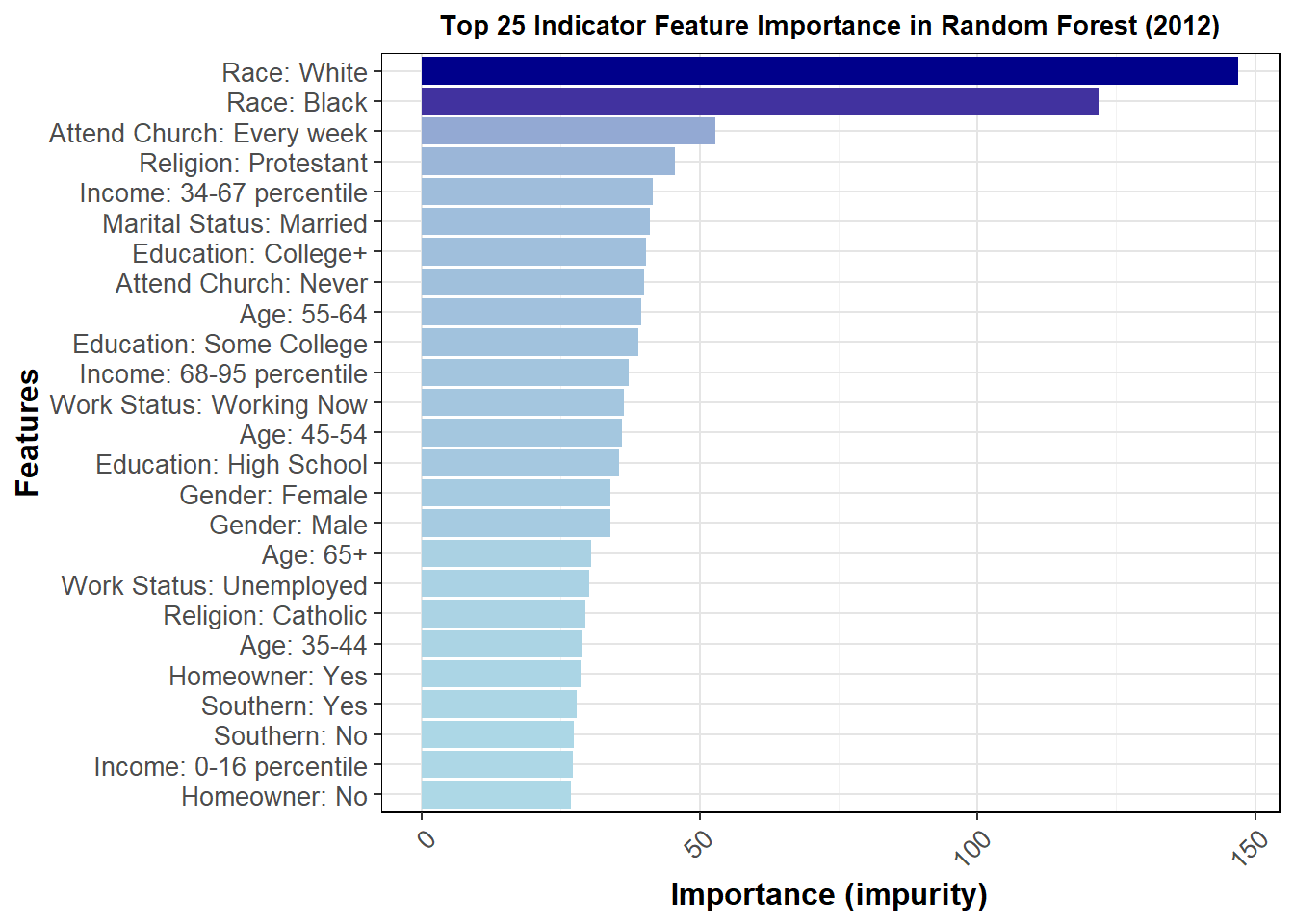
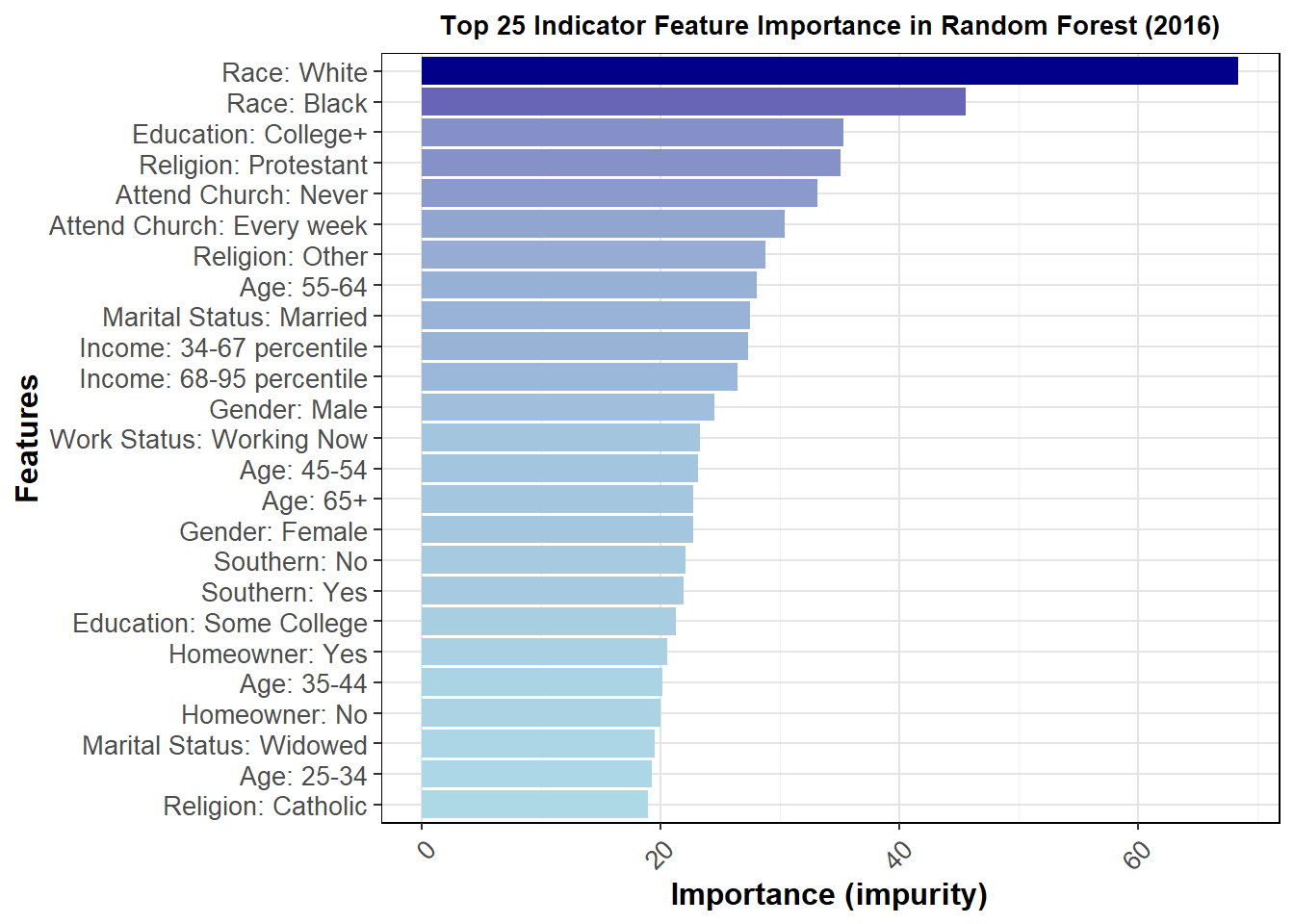
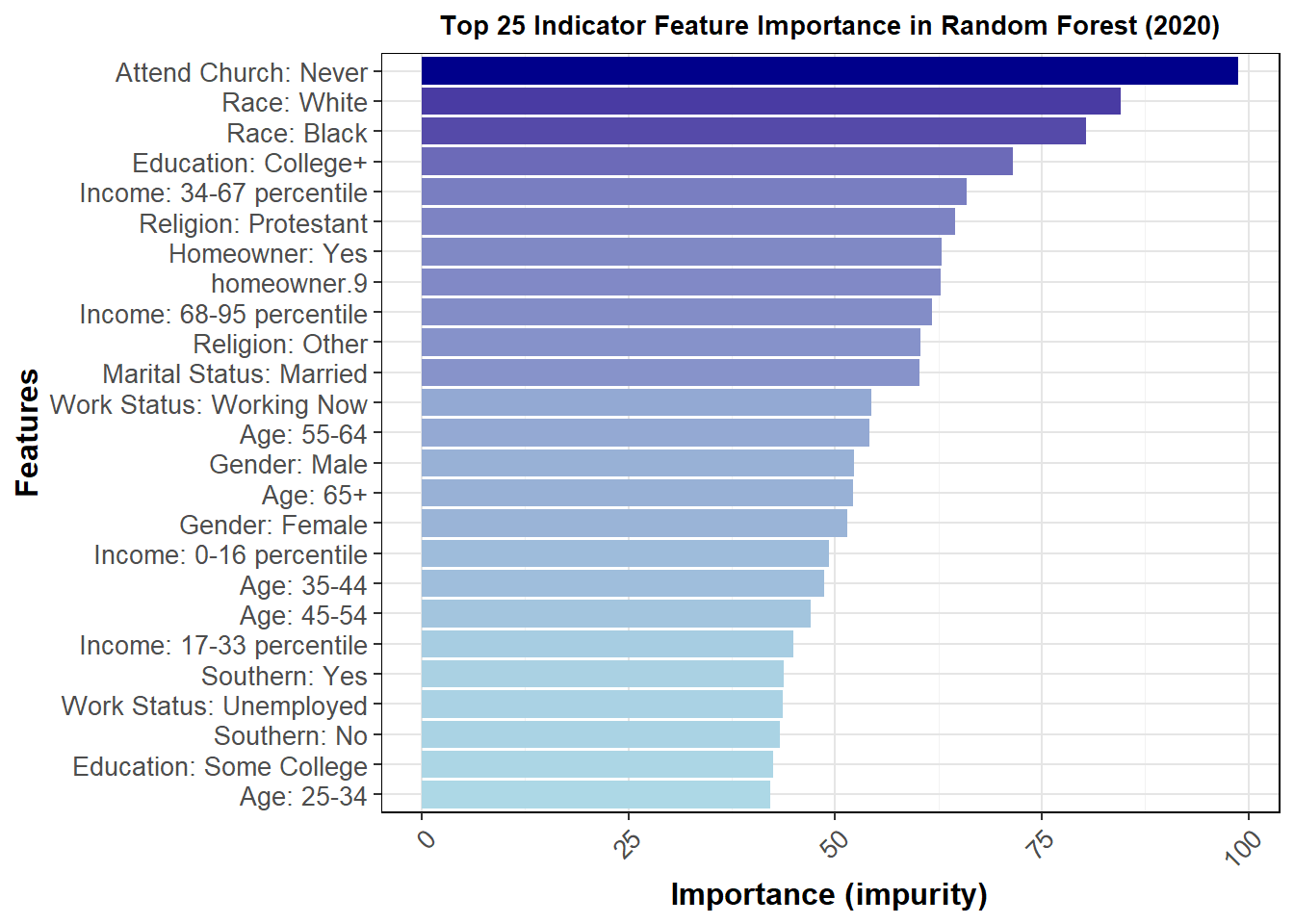
The general feature importance is mostly consistent across years. It does appear that the top 25 most important features are somewhat different, at least in order, over the three most recent elections, further pointing to demographic data as difficult to use in terms of accuracy of prediction. For this reason, I will not be using demographics to directly calculate vote share in my model, though as discussed in the next section it may be helpful for determining 2024 turnout. The full interpretations of these graphs and their important will be more fully explored in my presentation for this week.
Before moving on to my model for the week, I turn to the random forest model of turnout, as I did with presidential vote share. As I discuss below, turnout is hard to measure across years due to no significant 2024 demographic data and other questions on how turnout chnages each year, but for now I look at 2012-2020 to understand the factors that impact it. My turnout model in my simulation will be simple, but these insights can be drawn on for the future to make a more significant turnout model.
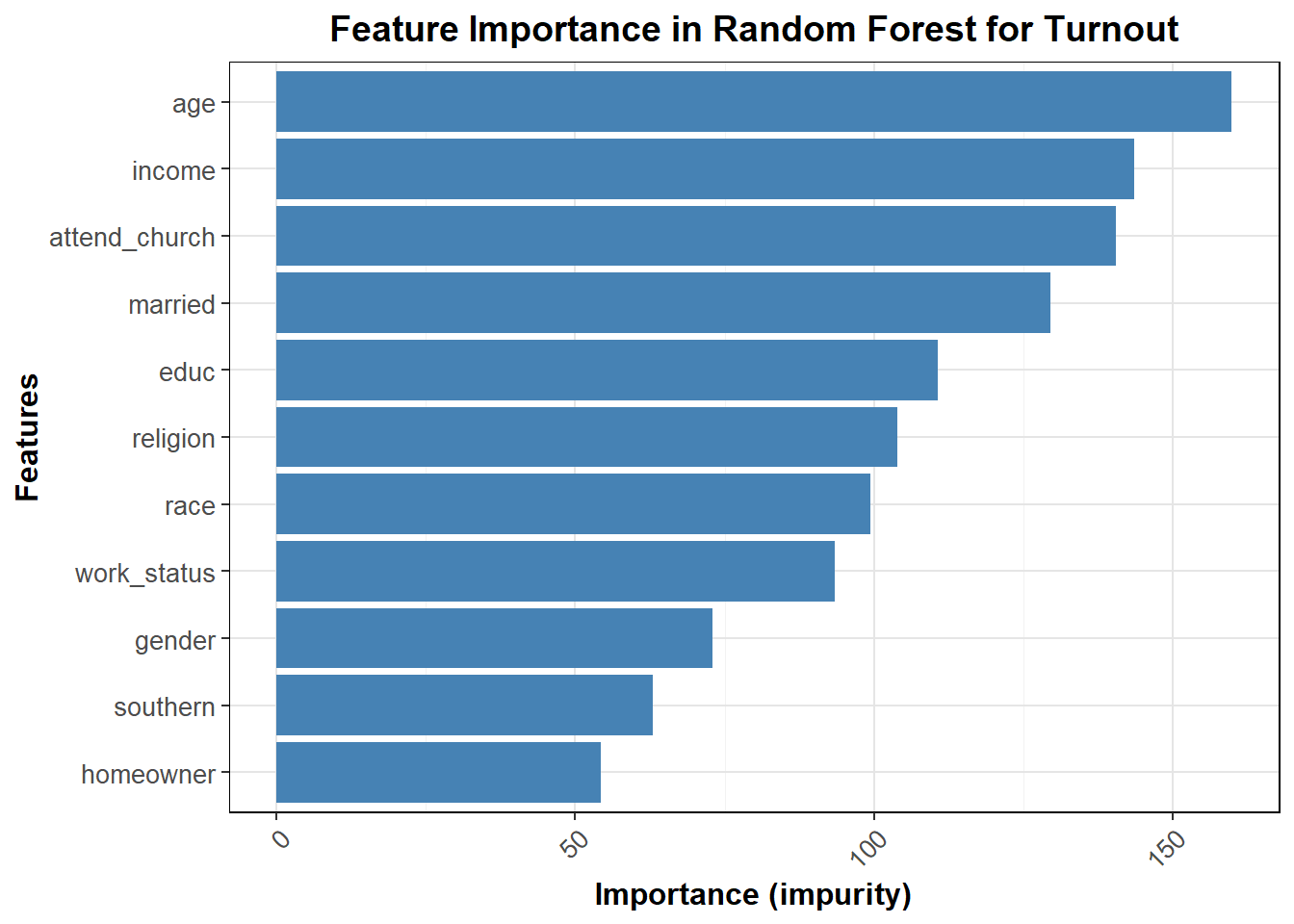
The random forest model for turnout in 2016 shows that age, income, and church attendance are the most important predictors of voter turnout. Variables like gender, southern residence, and homeownership have less predictive power in comparison to the top features. Remember, in a random forest, impurity measures how mixed or “impure” the data is at a given node, with lower impurity indicating more homogeneity; feature importance is determined by how much each variable reduces impurity, meaning the most important features are those that most effectively split the data into pure or homogeneous groups.
Looking at the confusion matrices below, I see an accuracy of demographic variables alone in sample of 64.11% and out of sample of 62.41%, performing worse than tha logistic regression and having less predictive power on this than vote share. Note that did not vote is the positive class below.
| Did Not Vote | Voted | |
|---|---|---|
| Did Not Vote | 514 | 440 |
| Voted | 773 | 1592 |
| Did Not Vote | Voted | |
|---|---|---|
| Did Not Vote | 138 | 108 |
| Voted | 181 | 403 |
I can also split across features as indicators of each level of a variable. For 2016, the top 25 are seen below.
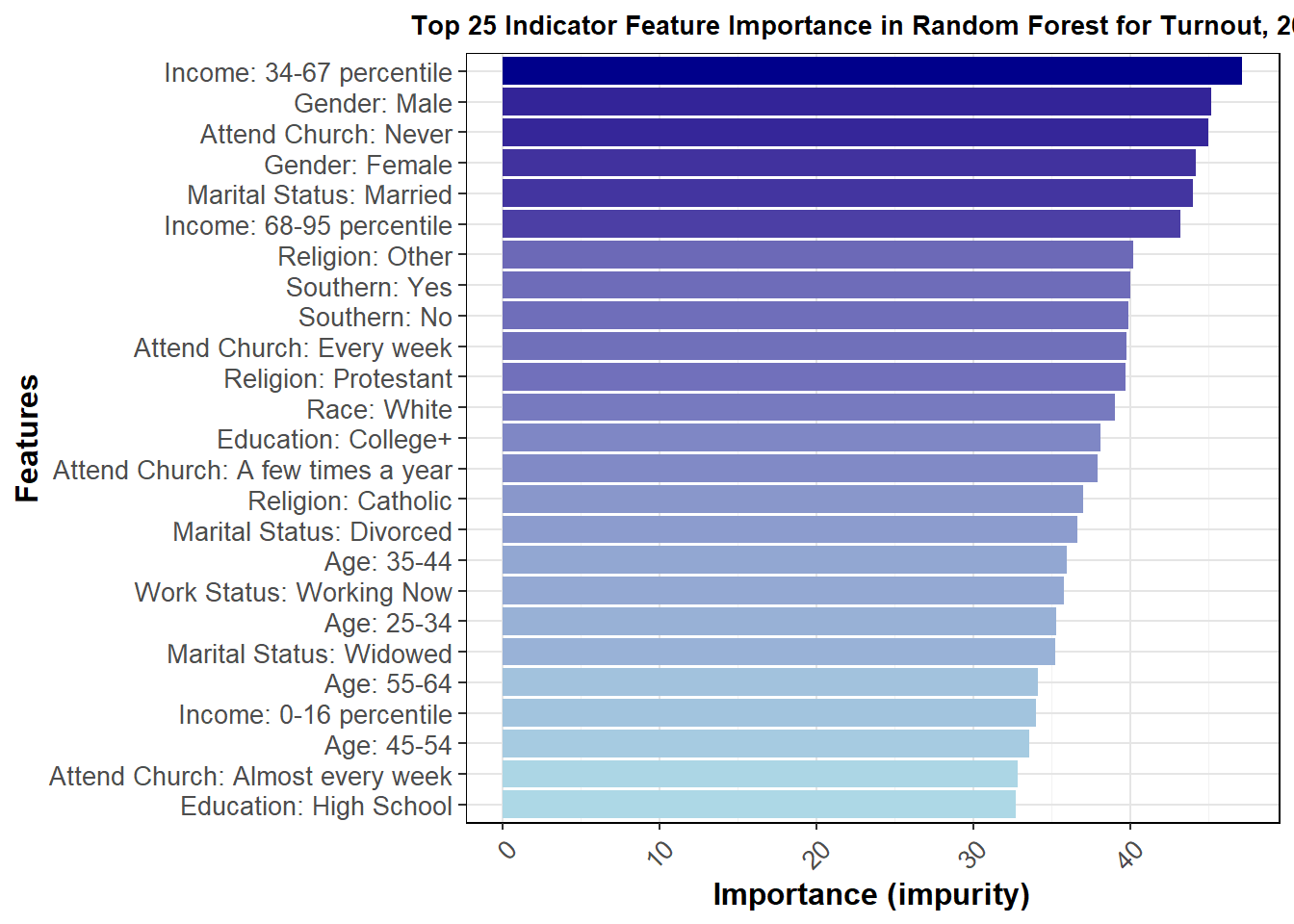
This graph gives us insight into which groups were most important at determining turnout, but not this is not causal. Because the above only looks at 2016, I thought it would also be important to see how much this changes for 2012 and 2020.
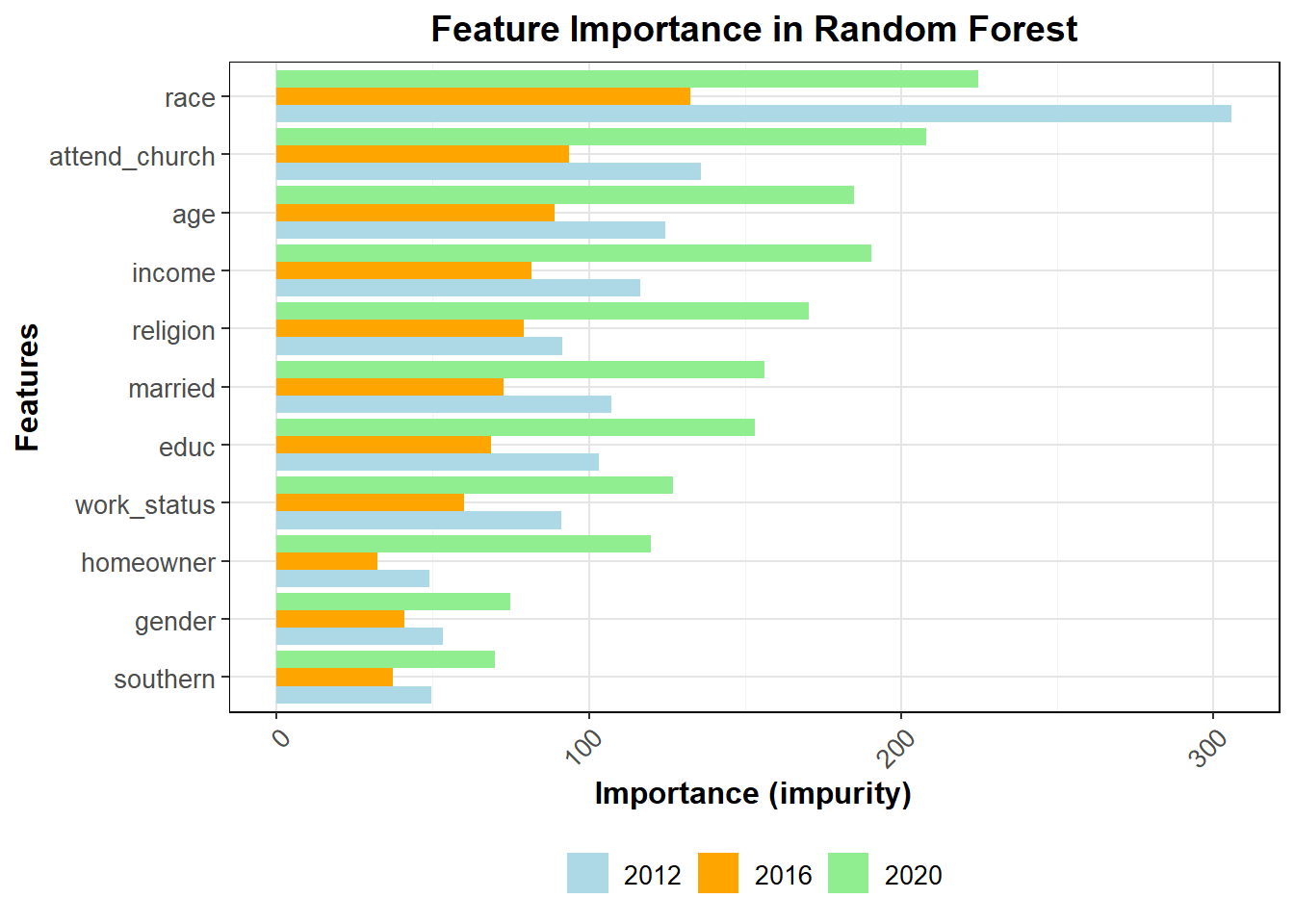
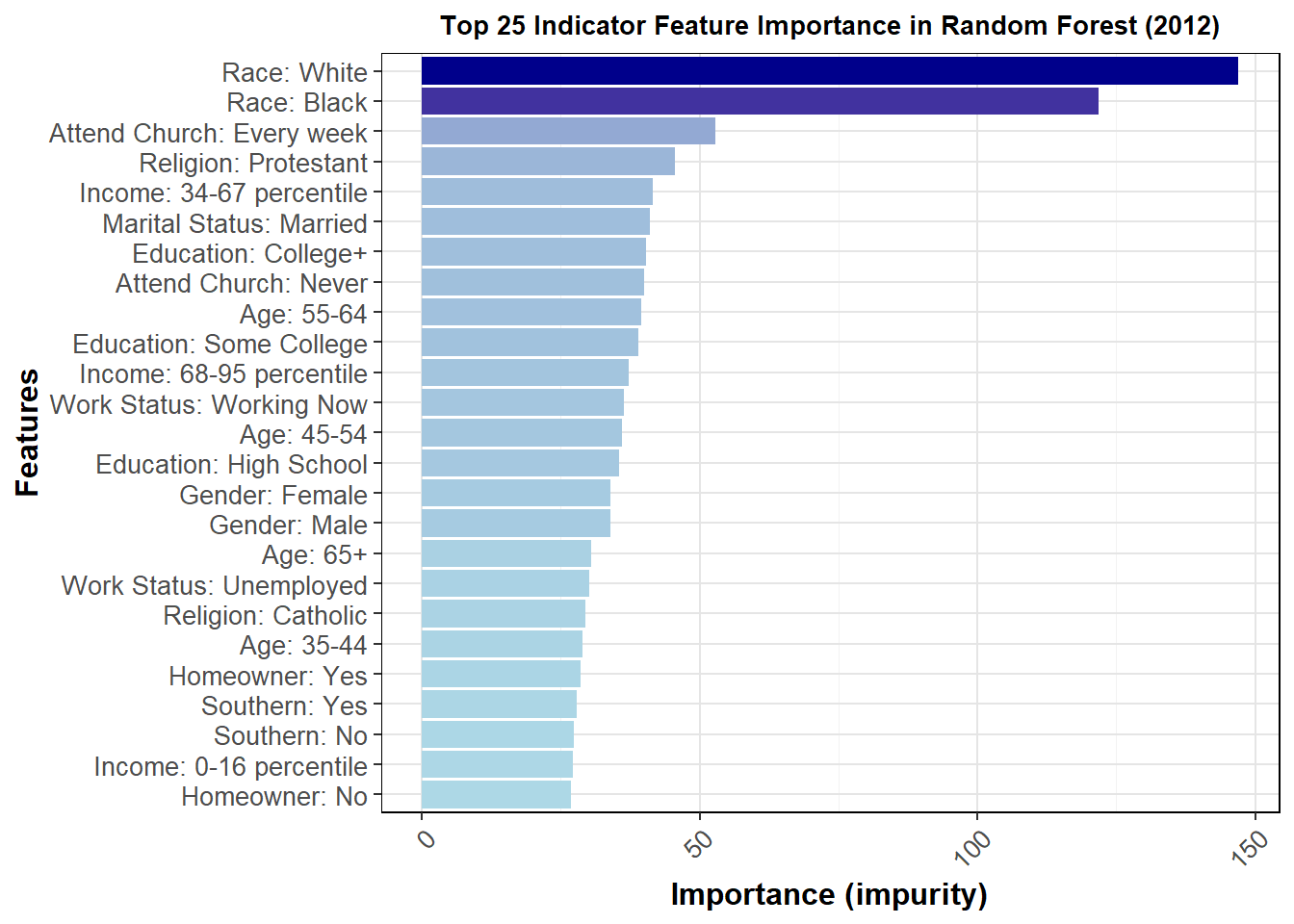
The general feature importance is somewhat consistent across years. It does appear that the top 25 most important features are somewhat different, at least in order, over the three most recent elections, further pointing to demographic data as difficult to use in terms of accuracy of prediction. Demographics can somewhat help predict turnout, but it does not seem strong enough to warrant strong inclusion in my model. I may include demographics as a predictor of turnout in a future iteration, but as discussed below my model this week uses historical weights.
Simulating the Outcome
Simulation is a powerful statistical technique used to model complex systems by generating random samples that represent real-world phenomena. In the context of voting behavior, simulations can help us predict election outcomes by running models that utilize a normal distribution. Prominent organizations like FiveThirtyEight (538) employ these techniques to enhance their election predictions. By simulating, we incorporate uncertainties to better understand potential electoral outcomes.
Calculating voter turnout is inherently challenging due to the myriad of factors that influence voter participation, as seen above. In this simulation, I must address the issue of estimating turnout for 2024, given that the dataset lacks specific demographic information for that year. I also don’t know exactly who will turnout out for this election.
To deal with this, we have several options: estimate state-level demographics from voter files, interpolate Census demographics using a statistical model, or simulate plausible values for turnout based on historical averages or advanced modeling techniques. For this analysis and simplicity, I chose to simulate turnout values by drawing from historical averages, recognizing that a demographic-based method may yield only around 70% accuracy, as demonstrated in earlier sections.
I present simulated predictions for only the seven states of interest.
| state | mean_dem | lower_dem | upper_dem | mean_rep | lower_rep | upper_rep |
|---|---|---|---|---|---|---|
| Arizona | 52.63265 | 52.07753 | 53.18777 | 52.97097 | 52.06249 | 53.87945 |
| Georgia | 53.33405 | 52.78584 | 53.88225 | 52.86964 | 51.97248 | 53.76680 |
| Michigan | 54.21094 | 53.66886 | 54.75301 | 50.41870 | 49.53157 | 51.30583 |
| Nevada | 53.40772 | 52.85842 | 53.95702 | 51.51443 | 50.61548 | 52.41339 |
| North Carolina | 52.65471 | 52.10302 | 53.20640 | 53.52056 | 52.61770 | 54.42343 |
| Pennsylvania | 53.35639 | 52.80526 | 53.90753 | 51.63047 | 50.72852 | 52.53243 |
| Wisconsin | 53.92703 | 53.37558 | 54.47848 | 51.08031 | 50.17784 | 51.98278 |
In this analysis, I simulated potential election outcomes for 2024 across all states but focused on specific battleground states for detailed results. The simple model utilized historical voting data and polling averages to predict vote shares for both Democratic and Republican candidates. Key variables in the model include D_pv2p_lag1 and D_pv2p_lag2, which capture the lagged Democratic vote shares from the previous two elections, indicating historical voting behavior. latest_pollav_DEM and mean_pollav_DEM reflect the most recent and average polling data for Democrats, showcasing current voter sentiment. Additionally, vep_turnout estimates eligible voter turnout, which is crucial for electoral outcomes, while economic factors like GDP_growth_quarterly and RDPI_growth_quarterly assess the overall economic environment and represent the economic fundamentals carried through from past weeks. This model is a continuation the two variables I have chosen to pursue as useful in my predictions: economic fundamentals and polling data. The simulations were carried out by varying turnout estimates drawn from historical averages, enabling us to incorporate uncertainty in turnout predictions.
In the simulation results, I see that the predicted vote shares for Democratic and Republican candidates exceed 100%. This occurs because the model calculates each party’s vote share independently, reflecting distinct voter preferences and turnout estimates. The predictions are also not all statistically significantly different, and within that margin of error the winner is not predicted, so for this week’s prediction I will pick the one with the higher mean value as the winner if they are within each other’s prediction interval, giving:
Arizona: R Georgia: D Michigan: D Nevada: D North Carolina: R Pennsylvania: D Wisconsin: D
Note that Michigan, Pennsylvania, Wisconsin, and Nevada were statistically significantly different, while others are still indeterminable by the simulations. Below I plot the distribution of values for each in the simulations.
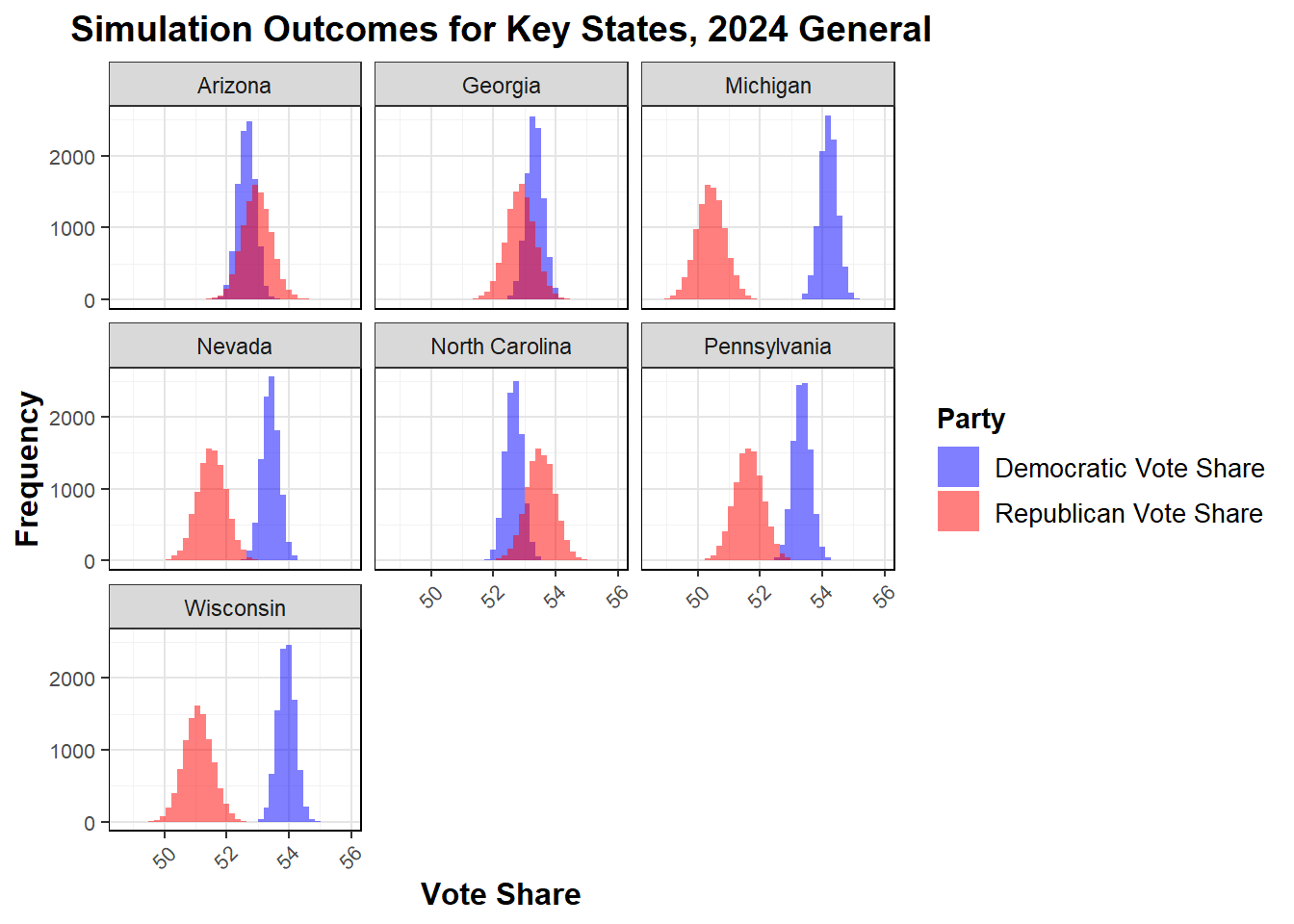
It appears that Democratic vote share is more clustered, while Republican is more distributed with a larger standard deviation. As a result of all of this, I can now make my new prediction, which is different by a state (Arizona to Republican) from my prediction from last week.
Current Forecast: Harris 292 - Trump 246
Data Sources
- Popular Vote Data, national and by state, 1948–2020
- Electoral College Distribution, national, 1948–2024
- Demographics Data, by state
- Primary Turnout Data, national and by state, 1789–2020
- Polling Data, National & State, 1968–2024
- FRED Economic Data, national, 1927-2024
- ANES Data, national
- Voter File Data, by state