Today marks 17 days until election day. As such, this week’s post will focus on bringing together all of the work I have done so far in determining predictors and building and forecast for the 2024 presidential election outcome. Beginning with a review of my past models, I will update them based on new polling data and use additional model evaluation techniques to understand their current performance. Following this, I explain decisions for choosing certain predictors, ensembling methods, and create a new probability-based turnout prediction rather than a simple weighted average of past turnout. Finally, I try a new model, using binomial simulations to compare to my chosen modeling technique. By the end of this post, I will have determined my base model for the next two weeks to fine tune as I attempt to predict the outcome of the election.
Review of Past Forecasting Models
In this section, I review the forecasting models developed throughout weeks 1 to 6. Each model was built with a unique combination of variables and assumptions, leading to varying results. By walking through the results and calculations from each week, I reflect on which model performed best and why. I also update the models with the newest polling data and introduce new evaluation techniques.
Because these models were made up to six weeks ago, the polling inputs have changed, particularly in those that use most recent polling data and average poll numbers. This helps determine if my eventual preferred model still holds up or if adjustments are necessary to account for new information.
Below are the results from each week’s model, as well as those that have been updated with new polling.
Week 1: This week used a simplified Norpoth model to make a prediction based on a weighted average of the election results from 2016 and 2020 by state. The predictive model can be defined as \(vote_{2024} = 0.75vote_{2020} + 0.25vote_{2016}\). This forecast resulted in Harris 276 - Trump 262.
Week 2: This week focused on economic variables and linear regressions. Evaluating a variety of economic fundamentals as predictors of two way popular vote, I found Q2 GDP growth in the election year to be the best predictor by on R sqaured, RMSE, and a variety of other linear model evaluations as compared to other economic variables. This forecast focused on two way popular vote, leading to a result of Harris 51.585% - Trump 48.415%.
Week 3: The main two models developed this week were ensembled elastic net regression models that weighed fundamentals more closer to the election and weighed polling more closer to the election. The final forecast for this week was an unweighted average between the two, leading to Harris 51.0645% - Trump 50.1031%. Updated with new polling data, I can compare the original and new predictions based on this method
| Party | Prediction |
|---|---|
| Polls More | |
| Harris | 51.71210 |
| Trump | 50.22182 |
| Fundamentals More | |
| Harris | 51.31497 |
| Trump | 50.00100 |
| Unweighted | |
| Harris | 51.06450 |
| Trump | 50.10310 |
| Party | Prediction |
|---|---|
| Polls More | |
| Harris | 52.61113 |
| Trump | 50.77154 |
| Fundamentals More | |
| Harris | 51.65896 |
| Trump | 48.59975 |
| Unweighted | |
| Harris | 52.13505 |
| Trump | 49.68565 |
Week 4: During this week, I began to narrow my work only down to the seven critical states: Arizona, Georgia, Michigan, Nevada, North Carolina, Pennsylvania, and Wisconsin. The model used was a super-learning model, leading to Harris 303 - Trump 235. The predictors used were polling, economic fundamentals, and lagged vote share of 2016 and 2020 in a pooled model. The updated model with new data is shown below.
| State | D Pop Vote Prediction | Winner |
|---|---|---|
| Wisconsin | 52.065 | D |
| Virginia | 54.521 | D |
| Texas | 49.048 | R |
| Pennsylvania | 50.554 | D |
| Ohio | 46.844 | R |
| North Carolina | 49.729 | R |
| New York | 61.434 | D |
| New Mexico | 54.052 | D |
| New Hampshire | 53.658 | D |
| Nevada | 50.794 | D |
| Nebraska | 42.888 | R |
| Montana | 46.077 | R |
| Missouri | 44.025 | R |
| Minnesota | 51.82 | D |
| Michigan | 51.049 | D |
| Maryland | 62.501 | D |
| Georgia | 49.958 | R |
| Florida | 49.987 | R |
| California | 62.177 | D |
| Arizona | 50.159 | D |
These results are different from the previous week as they have Georgia going to the Republicans, leading to an updated prediction of Harris 287 - Trump 251.
Week 5: In week 5, I used a linear regression model with the predictors lagged popular vote, latest poll average, mean poll average, a weighted average of turnout, GDP quarterly growth, and RDPI quarterly growth. The results of two separate models led to predictions that added to above 100% for the combined vote share of the two parties, which I handled by comparing the two. My goal in this case was to get at solely electoral college, but updated this with a binomial model will be explored below. This was once again a pooled model. The results led to an outcome of Harris 292 - Trump 246 in the original simulations. Running new simulations, I get the below results
| state | mean_dem | lower_dem | upper_dem | mean_rep | lower_rep | upper_rep |
|---|---|---|---|---|---|---|
| Arizona | 52.33565 | 51.93738 | 52.73393 | 53.07533 | 52.24587 | 53.90480 |
| Georgia | 53.01701 | 52.61740 | 53.41663 | 52.94809 | 52.11582 | 53.78035 |
| Michigan | 53.52168 | 53.12446 | 53.91890 | 50.83952 | 50.01225 | 51.66679 |
| Nevada | 52.95462 | 52.55830 | 53.35095 | 51.64988 | 50.82447 | 52.47530 |
| North Carolina | 52.65412 | 52.25402 | 53.05422 | 52.81871 | 51.98545 | 53.65197 |
| Pennsylvania | 53.37834 | 52.97970 | 53.77698 | 51.35816 | 50.52793 | 52.18839 |
| Wisconsin | 53.40013 | 52.99990 | 53.80035 | 50.99817 | 50.16464 | 51.83171 |
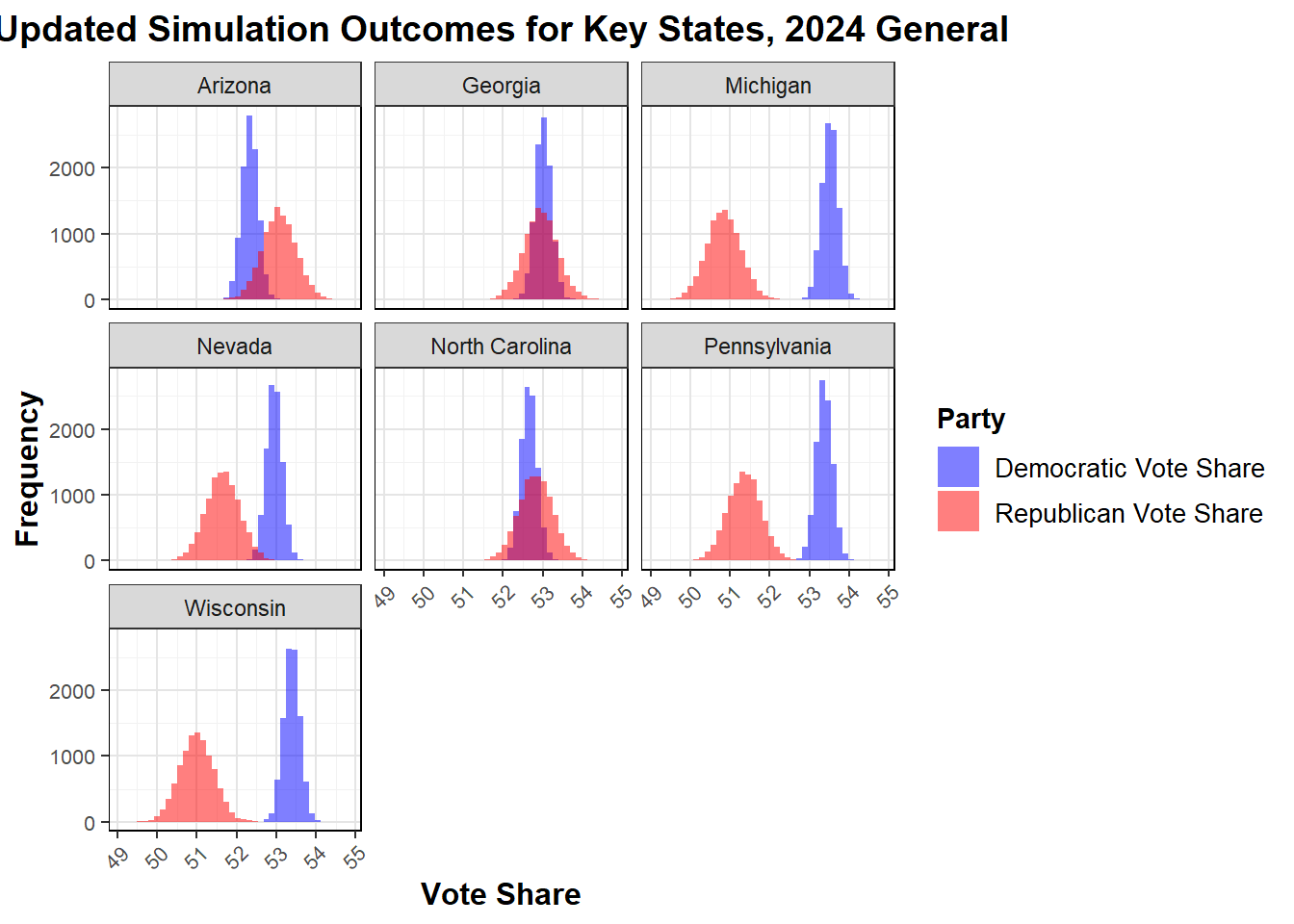
From these outcomes, I can see that the states with popular vote values predicted outside of the prediction interval to go for one party or the other are Michigan, Nevada, Pennsylvania, and Wisconsin, all for the democrats. For states within the margin of the prediction interval, I have Arizona (R), Georgia (D), and North Carolina (R). This does not differ from my original week 5 prediction by any state, but the margin has gotten larger in favor of Republicans in Arizona, smaller for democrats in Georgia, Michigan, Nevada, Pennsylvania, and Wisconsin, smaller for Republicans in North Carolina, based solely on comparing the mean predicted vote shares from the simulations.
Week 6: This week maintained the same prediction from last week, but urged inclusion of FEC contributions data in future models to see if it improves fit. The prediction remained Harris 292 - Trump 246.
As next steps for the following weeks, there are additional new model evaluation techniques in addition to those used in past posts to consider. Looking forward, I will improve predictive accuracy and model robustness as a result of these. These techniques provide insight into how to help guide the direction of future refinements and eventual model choice.
Important Predictors to Include
In developing my election prediction model, I’ve decided to include economic fundamentals and polling data, both of which have consistently proven effective in past models. Moving forward, I plan to experiment with FEC data to see if it improves the each models’ fit. Another factor I may add is incumbency interaction effects, similar to what’s been used in super learning models. However, I’ve chosen to exclude certain variables like demographics, air war data (campaign ads), and ground war data (in-person campaigning) based on recent explorations showing limited predictive power in the persuasion space. Ground game data, in particular, has been difficult to gather, and according to Enos and Hersch (2015) and meta studies, the effect of on-the-ground strategies on persuasion is essentially zero. Their research found that campaign contacts may not have an effect potentially because persuasive messages don’t have longevity. This exclusion also aligns with meta-analyses showing that individual targeting does little to alter voter preferences.
However, I am adding ground game data in a separate turnout prediction model, as studies like Enos and Fowler (2016) suggest that ground efforts can increase turnout by as much as 6-7% in heavily targeted areas. For this reason, while I’m excluding ground game from my main model, I recognize its importance for predicting turnout, especially in combination with air war data from the final week of the campaign.
Additional decisions I have made include focusing my predictions on state-level outcomes in the seven swing states, which will then be aggregated to predict the overall Electoral College result. My model will use data from elections after 1964 rather than starting with 1952 or even pre-World War II. Given the changing landscape of election laws, I see this as a way to account for legal consistency is that has changed the electorate over time in the data I have.
Pooled, Unpooled, and Ensembling Notes
In my election prediction model, I plan to use pooled models, which combine data from multiple states and treat them as part of a single system, applying the same coefficients across all states to make predictions. This allows the model to capture correlations across states, meaning if we have more certainty about the result in one state, it can help improve predictions for others. Pooled models are especially useful because they rely on less data from individual states by “drawing strength” from states with more data, leading to more reliable predictions, even in data-sparse regions. Professional election forecasters often use these correlations to update one state’s prediction based on another’s outcome, enhancing the model’s adaptability as new information becomes available. There are also more advanced ways of pooling states together using techniques like clustering, which could improve the model’s ability to group similar states. I will consider these in future weeks.
Additionally, pooling offers the flexibility to combine pooled and unpooled models, or multiple pooled models, through ensembling, which blends different modeling approaches to capture their respective strengths. This allows the model to balance the benefits of pooled predictions with the more state-specific insights from unpooled models. By using appropriate checks on model performance, ensembling helps create a more accurate and balanced prediction by drawing from multiple perspectives. This combination of pooling and ensembling makes for a powerful approach that can improve the overall robustness of the election forecast. Both emsebling and pooled models were used in the models described in the previous sections descrbining my work from past weeks.
Adjusting Turnout Predictions
In the future, I plan to implement a more refined model to better predict voter turnout, addressing the lingering challenges caused by the unpredictability of COVID-19 and the widespread adoption of mail-in voting. These factors have created lasting shocks to turnout patterns that make forecasting difficult, and it’s clear from watching forecasts like FiveThirtyEight and The Economist that this unpredictability needs special handling. My approach will be to build probabilistic models that simulate fluctuations in turnout rather than using a fixed, static number for each state’s voter pool. For example, instead of setting each state’s maximum number of Binomial draws to the Voting Eligible Population (VEP) as I will do in the binomial simulations model below, I’ll draw a random number from a distribution based on VEP, while factoring in expected effects from vote-by-mail, early voting, and other dynamics. Additionally, this model will incorporate key variables such as demographics, ground game data, and air war data, all of which can have strong turnout effects. This approach will allow the model to adapt more flexibly to changes in voter behavior and the varying effectiveness of campaign strategies across states.
Binomial Simulations Model
My new model for this week will be binomial simulations. Whereas the linear regression model simulations may have values that do not add to 100%, this type of model addresses that.
Pennsylvania
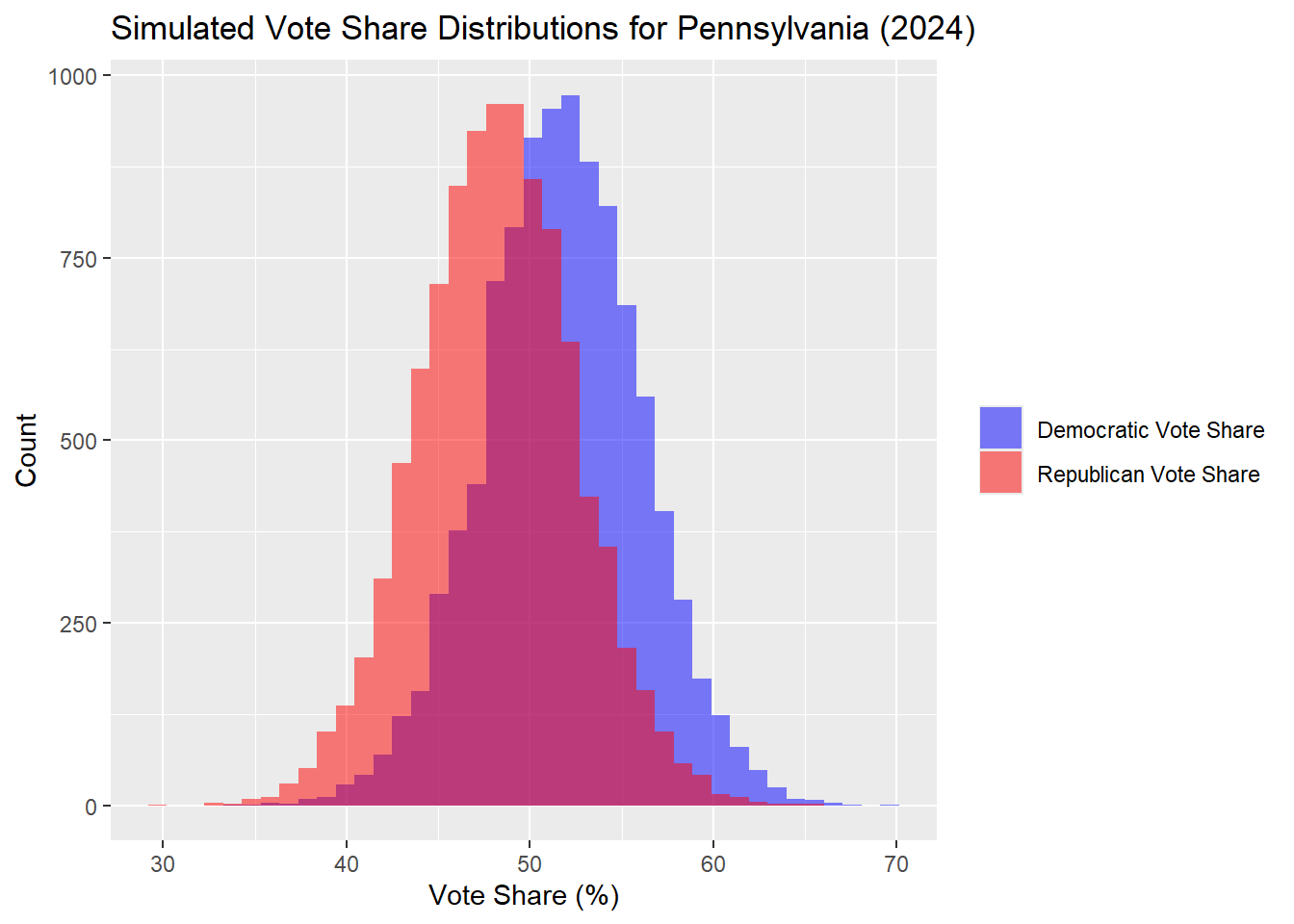
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -14.33 |
| 50% | Median | -3.56 |
| 90% | 90th Percentile | 7.31 |
Interpreting the simulated distributions, the blue density curve represents the distribution of simulated vote shares for Democrats. Since the peak of the blue curve is shifted more to the right than the red curve for the Republicans, that suggests that the Democratic vote share is predicted to be higher in more simulations. The fact that the curves are equally wide and tall implies that both parties face similar levels of uncertainty or variability in their predicted vote shares, but the model slightly favors Democrats in terms of likely outcomes. There is substantial overlap between the blue and red curves, meaning the model predicts a close race with both parties having a significant chance of securing similar vote shares. Note that this curve is only for the popular vote share outcome in Pennsylvania.
In the Pennsylvania outcomes, the median simulated outome was a Democrat popular vote share of 51.75% and Republican of 48.25%
I will now look at the results for each of the rest of the swing states:
Wisconsin
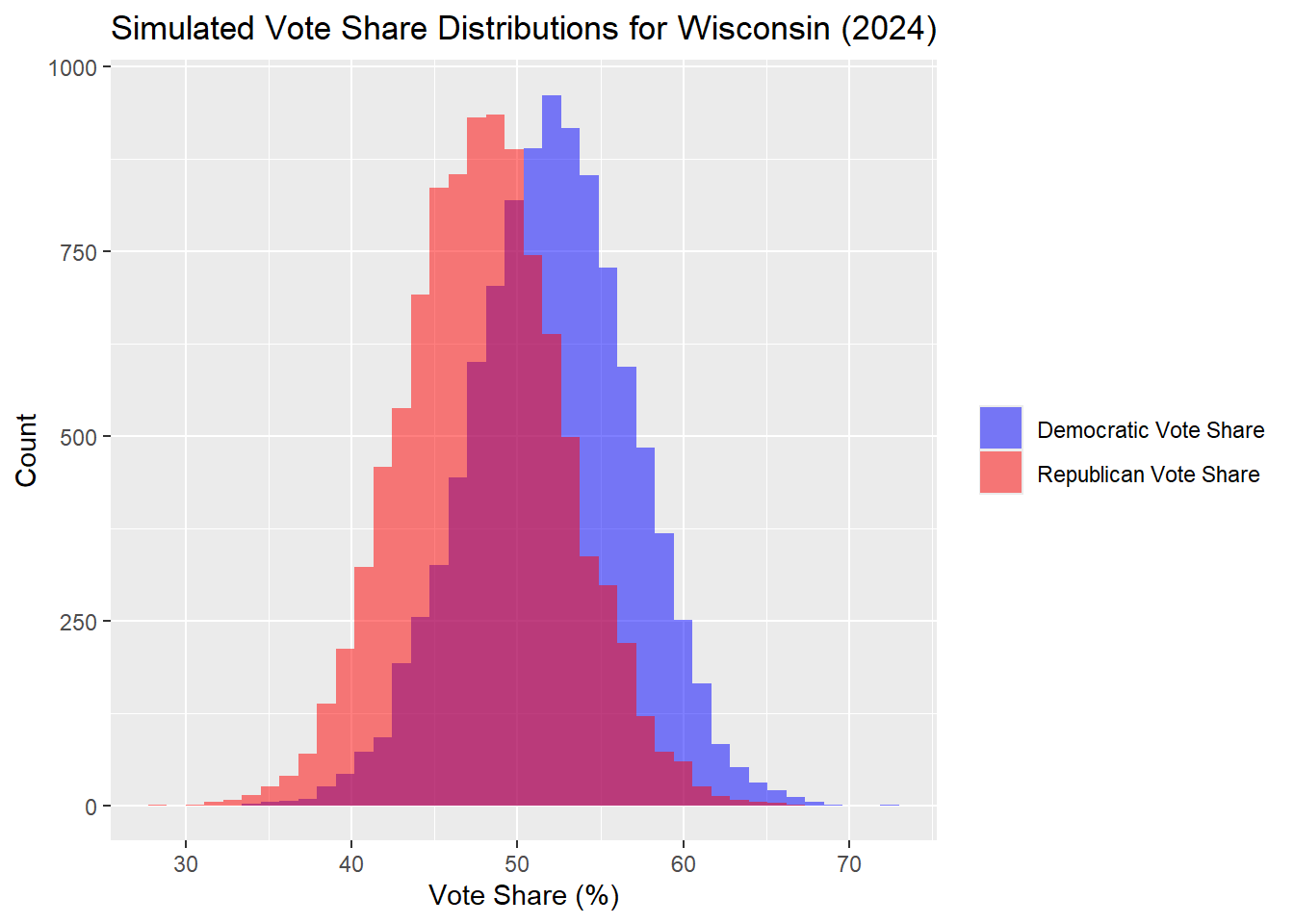
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -16.52 |
| 50% | Median | -4.15 |
| 90% | 90th Percentile | 8.50 |
The distributions above look similar to those for Pennsylvania, though they are slightly wider and therefore the outcome has a larger standard deviation. The median margin is also slightly bigger, but once again there is no clear winner with a 95% prediction interval. In the Wisconsin outcomes, the median simulated outcome was a Democrat popular vote share of 52.14% and Republican of 47.86%
North Carolina
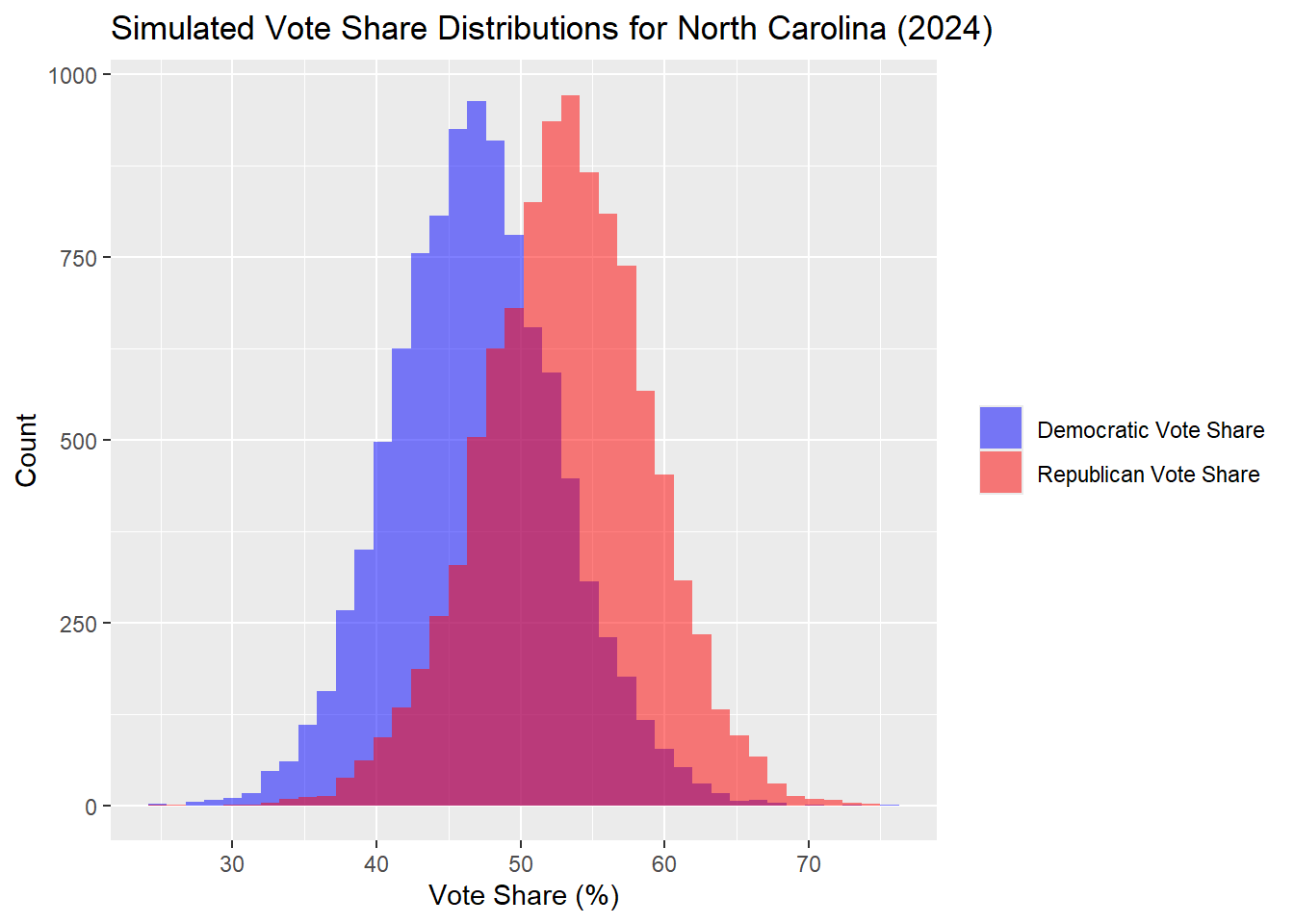
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -8.44 |
| 50% | Median | 6.40 |
| 90% | 90th Percentile | 20.62 |
In North Carolina, the Republicans do better in more simulations that Democrats. The distributions are again slightly wider and therefore the outcome has a larger standard deviation. The median margin is also bigger, this time in favor of the Republicans, and again there is no clear winner with a 95% prediction interval. In the North Carolina outcomes, the median simulated outcome was a Democrat popular vote share of 46.61% and Republican of 53.39%
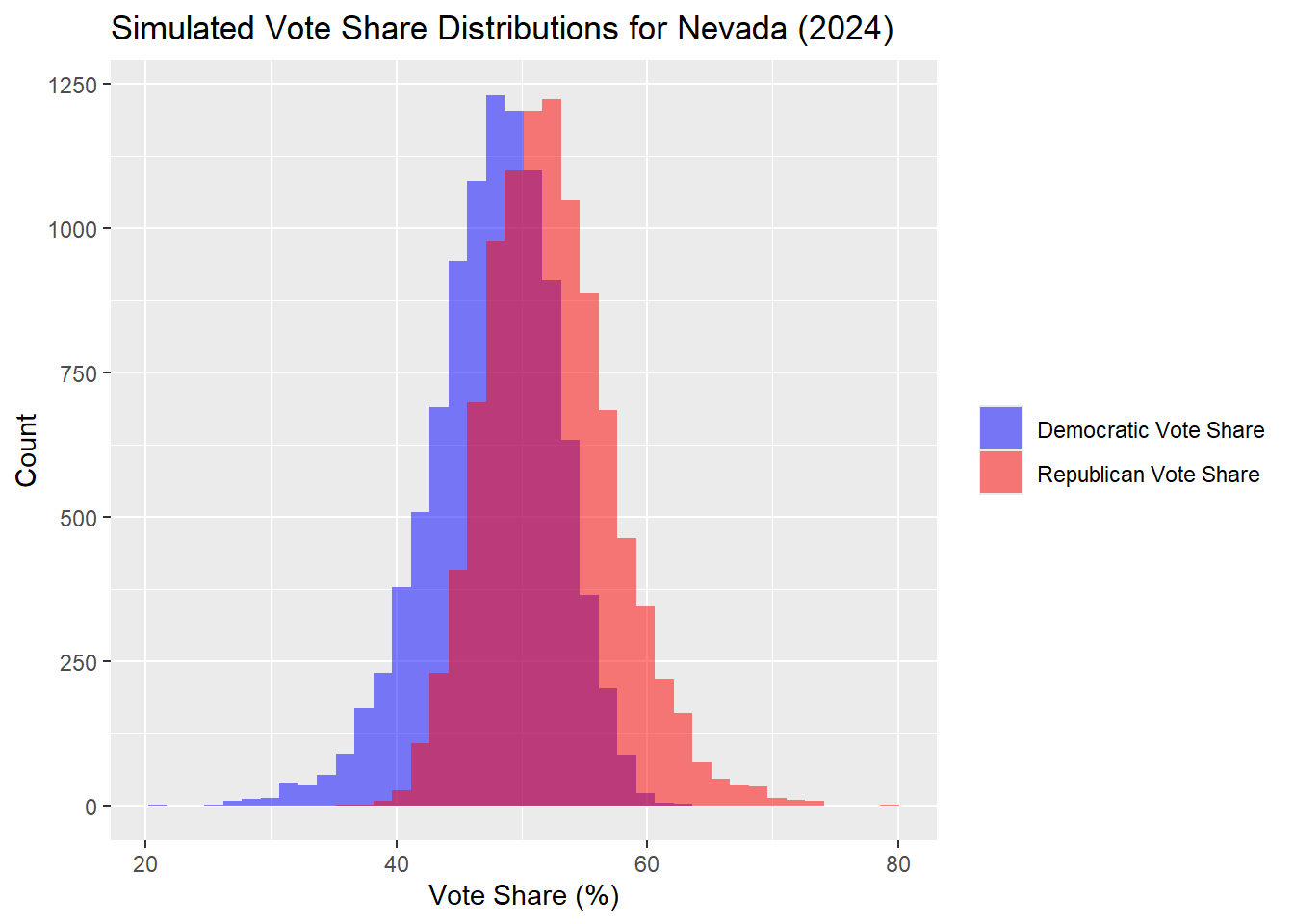
Nevada
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -7.52 |
| 50% | Median | 3.86 |
| 90% | 90th Percentile | 17.83 |
Once again, a 95% prediction interval for the margins include 0, so there is no clear winner. In the Nevada outcomes, the median simulated outcome was a Democrat popular vote share of 47.93% and Republican of 52.07%. It is worth noting that this result is distinctly different from both of my previous models I ran simulations for, so Nevada has flipped Republican in this case, but within the margin of error.
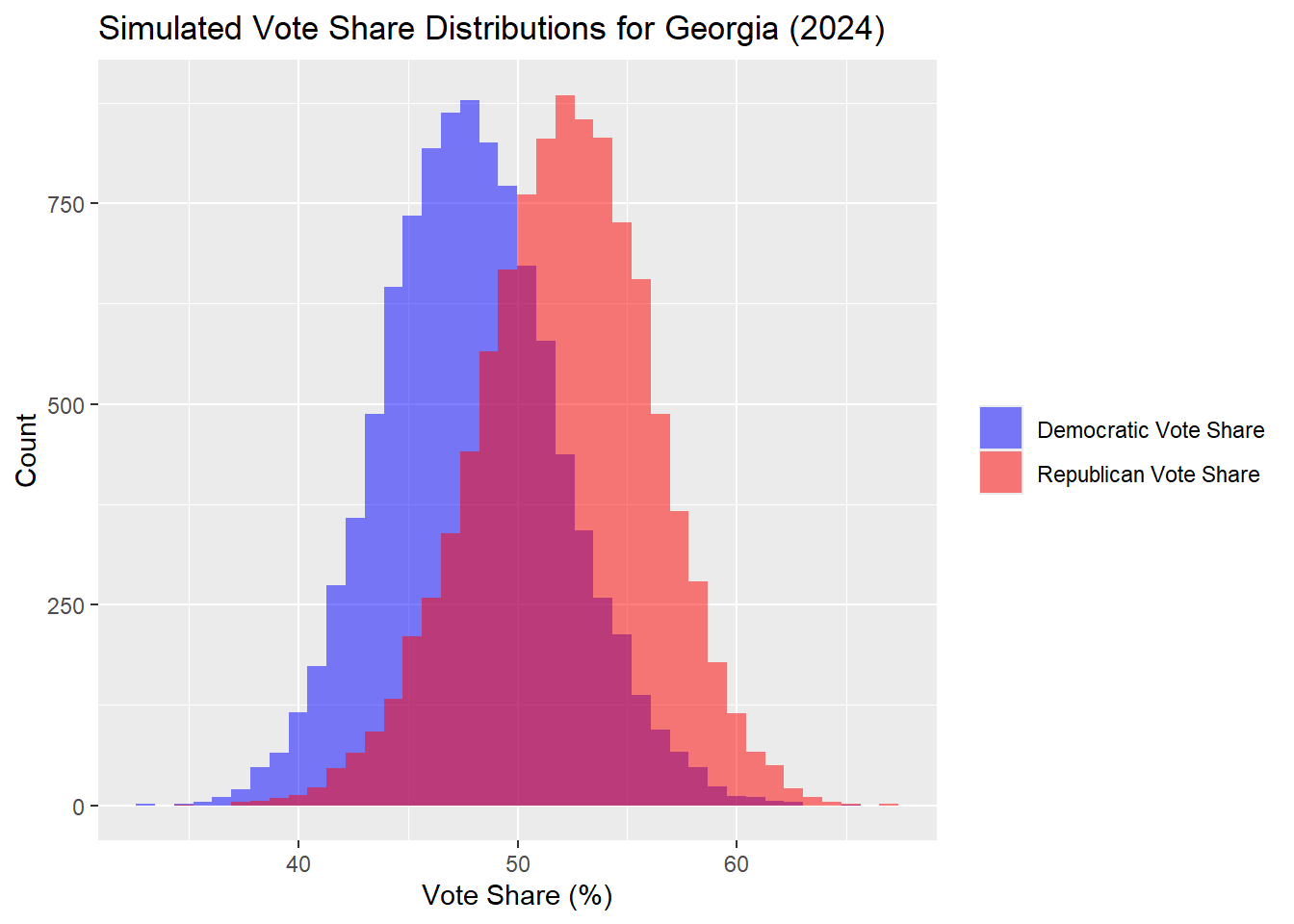
Georgia
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -6.22 |
| 50% | Median | 4.51 |
| 90% | 90th Percentile | 14.23 |
Once again, a 95% prediction interval for the margins include 0, so there is no clear winner. In the Georgia outcomes, the median simulated outcome was a Democrat popular vote share of 47.73% and Republican of 52.27%. It is worth noting that this result is distinctly different from both of my previous models I ran simulations for, so Georgia has flipped Republican in this case, but within the margin of error.
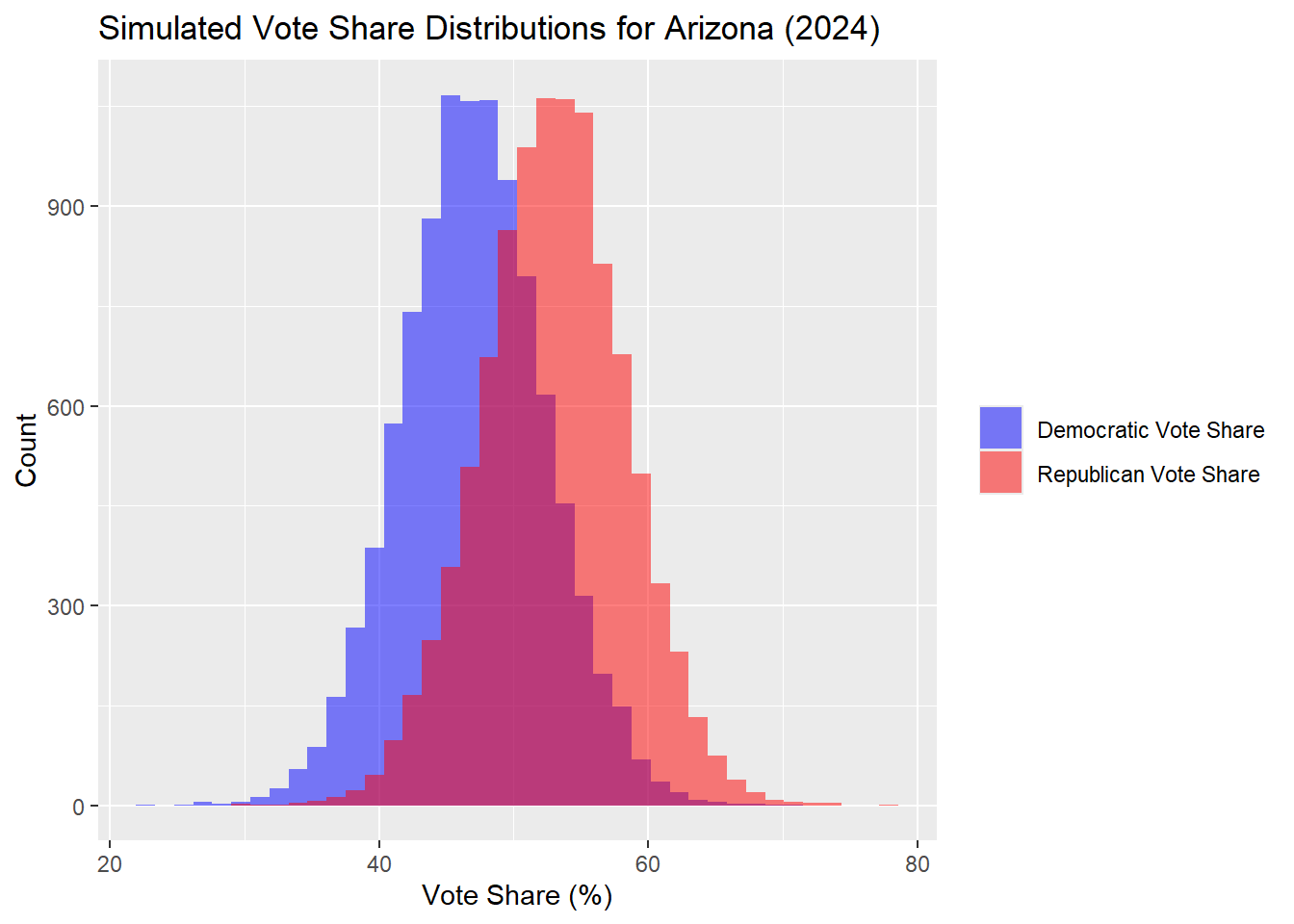
Arizona
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -7.70 |
| 50% | Median | 6.03 |
| 90% | 90th Percentile | 19.37 |
In the Arizona outcomes, the median simulated outcome was a Democrat popular vote share of 47.05% and Republican of 52.95%. It is worth noting that this result is distinctly different from both of my previous models I ran simulations for, so Arizona has flipped Republican in this case, but within the margin of error.
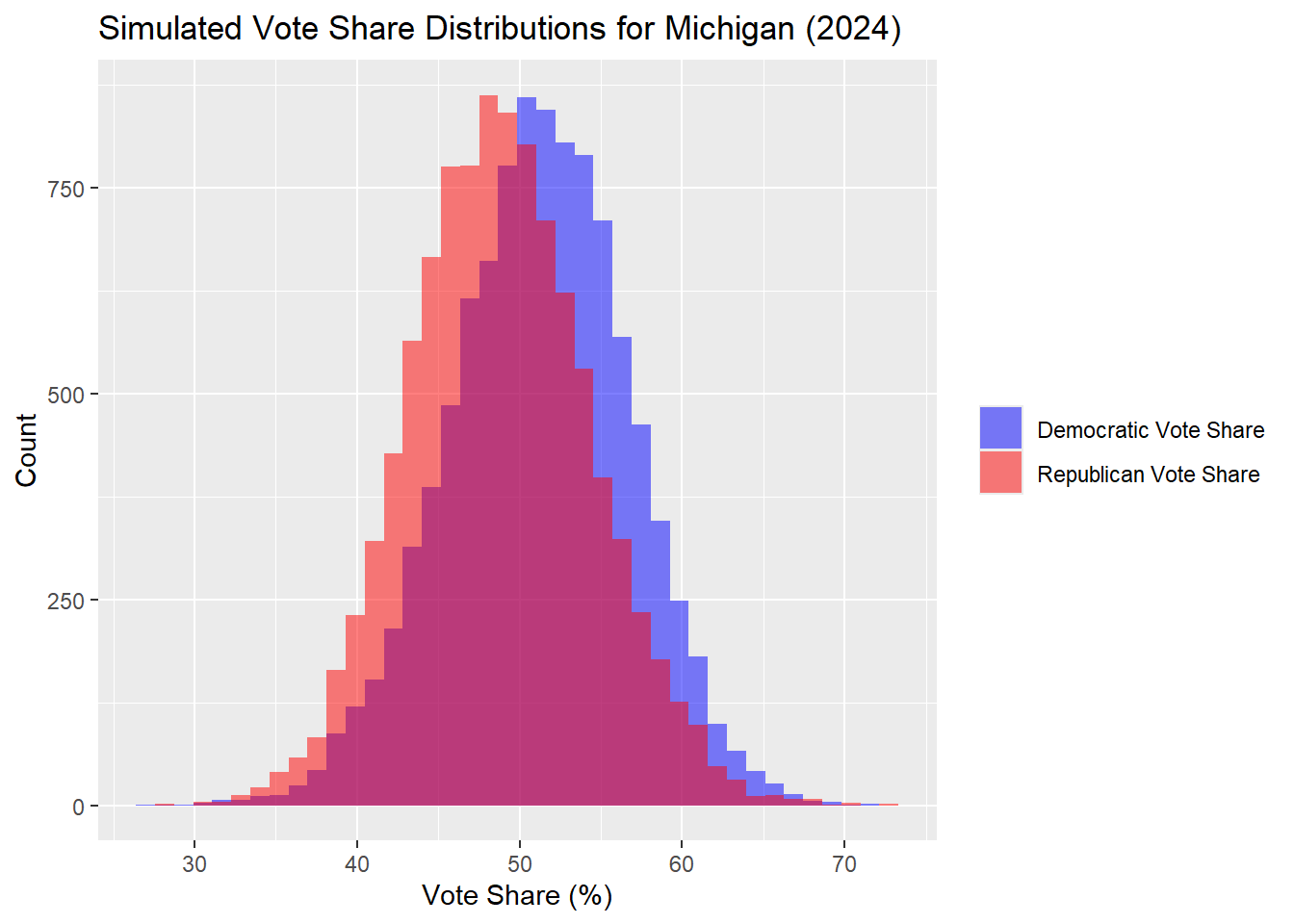
Michigan
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -16.36 |
| 50% | Median | -2.67 |
| 90% | 90th Percentile | 11.96 |
In the Michigan outcomes, the median simulated outcome was a Democrat popular vote share of 51.4% and Republican of 48.6%. This remains for the Democrats, within the margin of error.
Using the above binomial models and new turnout modeling using a weighted average of the prediction of the voter eligible population from a general additive model and OLS regression, three states have flipped from my past models. I now have the results:
Wisconsin: D
Pennsylvania: D
North Carolina: R
Nevada: R
Georgia: R
Arizona: R
Michigan: D
This leads to a predicted electoral college outcome of Harris 270 - Trump 268.
Notes of Bayesian Approaches
Although I initially planned to compare my model with a Bayesian approach using MCMC, I decided not to proceed with Bayesian methods for now. Bayesian models are useful because they allow for incorporating prior information and uncertainty into predictions, making them valuable for updating forecasts as new data becomes available. However, while some professional election forecasters use these models effectively, in my case, more complex approaches have not shown significant improvements over traditional OLS or time-for-change models. Given this, and the added complexity, I’m hesitant to explore them further at this stage.
This Week’s Prediction
This week, I ran out of time to add FEC contributions data into each model and then evaluate their fit, so this will be including in next week’s model choice post. For now, we have a large number of models, many of which agree on most states’ outcomes. As a result, I have chosen this week to take the two past week’s updated electoral college vote models, which result in Harris 287 - Trump 251 and Harris 292 - Trump 246, and the binomial simulations model, which gave Harris 270 - Trump 268, and average them (not possible in real electoral vote numbers) to get
Current Forecast: Harris 282 - Trump 256
Data Sources
- Popular Vote Data, national and by state, 1948–2020
- Electoral College Distribution, national, 1948–2024
- Turnout Data, national and by state, 1980–2022
- Polling Data, national and by State, 1968–2024
- FRED Economic Data, quarter 2
- Demographics, by state and county