In my last post before my final prediction, I will be exploring the final variables I must evaluate for inclusion in my model– those related to sudden shocks– and reviewing professional forecasts and what they have to say about the coming election. Additionally, I will tweak my binomial model specification, and test the in sample fit of my binomial and linear regression models.
Review of Professional Forecasts
As we draw closer to election day, many professional election forecasters have released their models for the race. Though each model yields a different result, many hover around the idea that the election is currently a toss-up, with some authors even using that language, even calling it a jump ball.
In the recent paper (unpublished) aggregating 12 forecasts, including the Tien and Lewis-Beck model, the average two party vote share predicted was 50.3% for Harris to 49.7% Trump. The electoral college was more clearly in support of Trump, giving him on average 292 electoral votes to Harris’ 246. They do note that these “forecasters are not fortune tellers” in their conclusion, but these models and their eventual comparison to the real outcome provides an especially useful look into how voters and campaigns act and react.
Specifically, the Lockerbie (2024) economic pessimism model (unpublished), one of those included in this aggregation, finds that time in the white house and whether people think the next year will be worse are important variables to include in the model, leading to low absolute errors in many years but outliers as large as 8.1 in 2020. These seem to be proxy variables for economic outlook and incumbency. Lockerbie uses “jump ball” to describe how this election could go, but does note that the model points to the presidency and house going together, which is consistent with our understanding of incumbent party cycles.
The Tien and Lewis-Beck (2024) political economy model (unpublished) measures incumbent party vote share by looking at presidential popularity and economic growth, weighting growth much higher. A potential issue with this model could be its reliance on July presidential approval, which would not reflect directly on Harris. The impact of this is unknown, and points to how I have been cutting the polling weeks for Harris versus Biden. Many others models predict similar jump ball outcomes for the election.
Review of Sudden Shocks
The last set of variables I considered including in my model were related to sudden shocks, which some may have heard of as something like an October surprise. However, I am looking much more broadly at both political and apolitical shocks. Apolitical shocks, including natural disasters, sports outcomes, and lottery winnings have all been shown to have some effect on support for incumbent candidates.
The common debate over whether sudden shocks effect voting is often talked about in context of Achen and Bartels’ 1916 paper on the effect of shark attacks in beach towns in New Jersey. They found the towns with these had less votes for the incumbents at a significant level compared to non-beach towns, which would not have been effected. However, Fowler and Hall (2018) refute this, pointing to an omitted town which takes away part of the effect and looking at all counties. The county that Achen and Bartels looked at, Ocean County, was an outlier, and Folwer and Hall found that beach towns and other voted very similarly.
It is also important to consider what the government could have changed in their response, as these apolitical shocks may not be so removed from politics. Healy and Malhotra (2010) found that the effects of the event on votes depend on whether there was any sort of disaster declaration, a potential variable to consider.
These and other shocks could have temporary or lasting, large or small effects on vote share, or perhaps on turnout. It is not unreasonable to believe that a natural disaster like the recent hurricanes in the important state of North Carolina could effect turnout in the region. Some other shocks discussed this week to consider with natural disasters were protests and Supreme Court cases. It is also worth noting that the effects of these may already be captured in polling or will be captured once I update my turnout model. For these reasons and those in the papers referenced above, I will not be including them in my model.
Tweaking the Binomial Model Specifications
Oringally, my binomial model’s only regressor was poll support. That resulted in the following predictions for each party’s vote share in each state based on hypothetical average polling data.
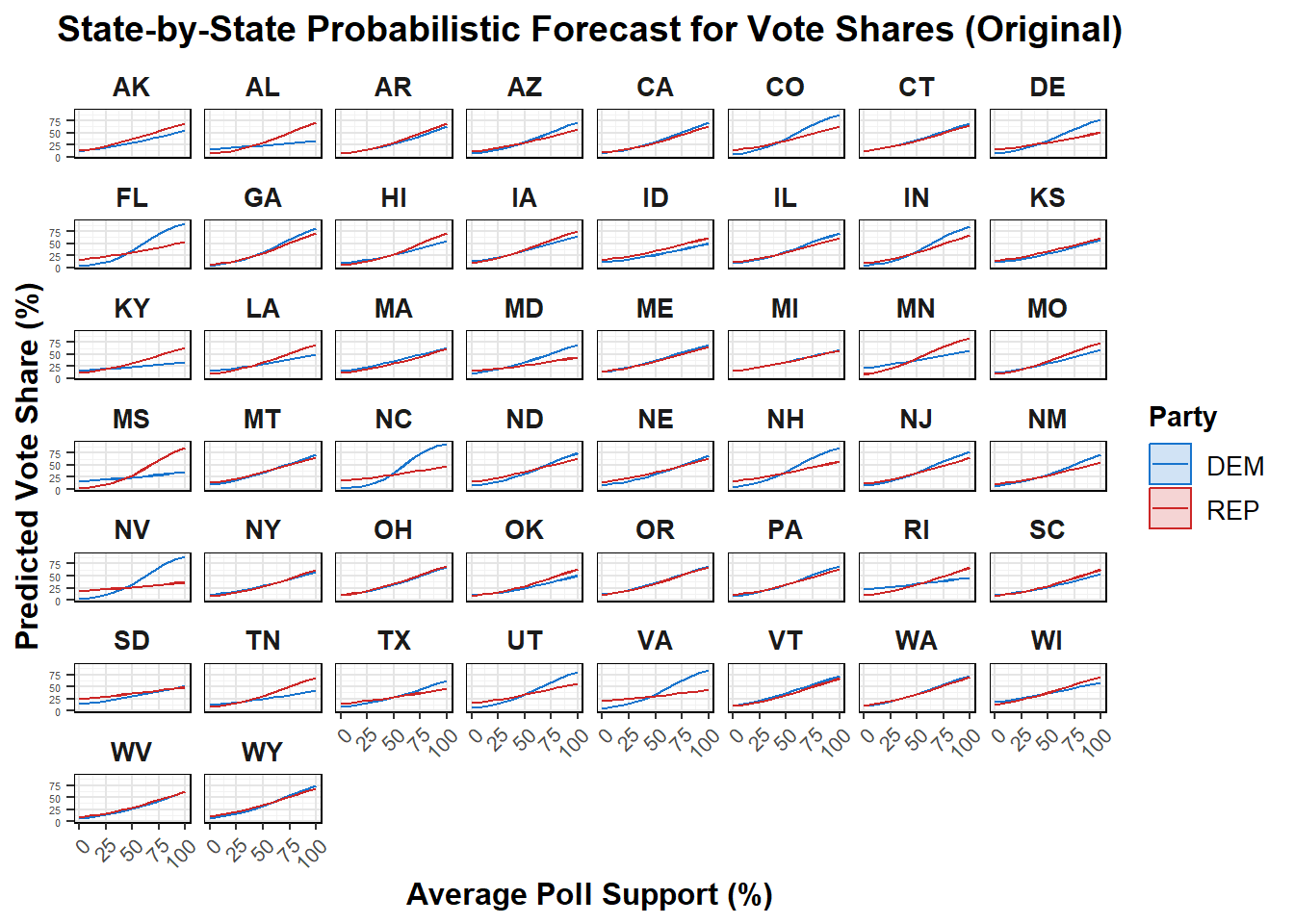
Because this only used poll support, and my models have been based off of fundamentals and polling, I created a new binomial regression using poll support, latest polling average, mean polling average, GDP growth quarterly, and RDPI growth quarterly, as I have in the past. The differing results from this model, as well as a more detailed interpretation of these graphs and the model, are below.
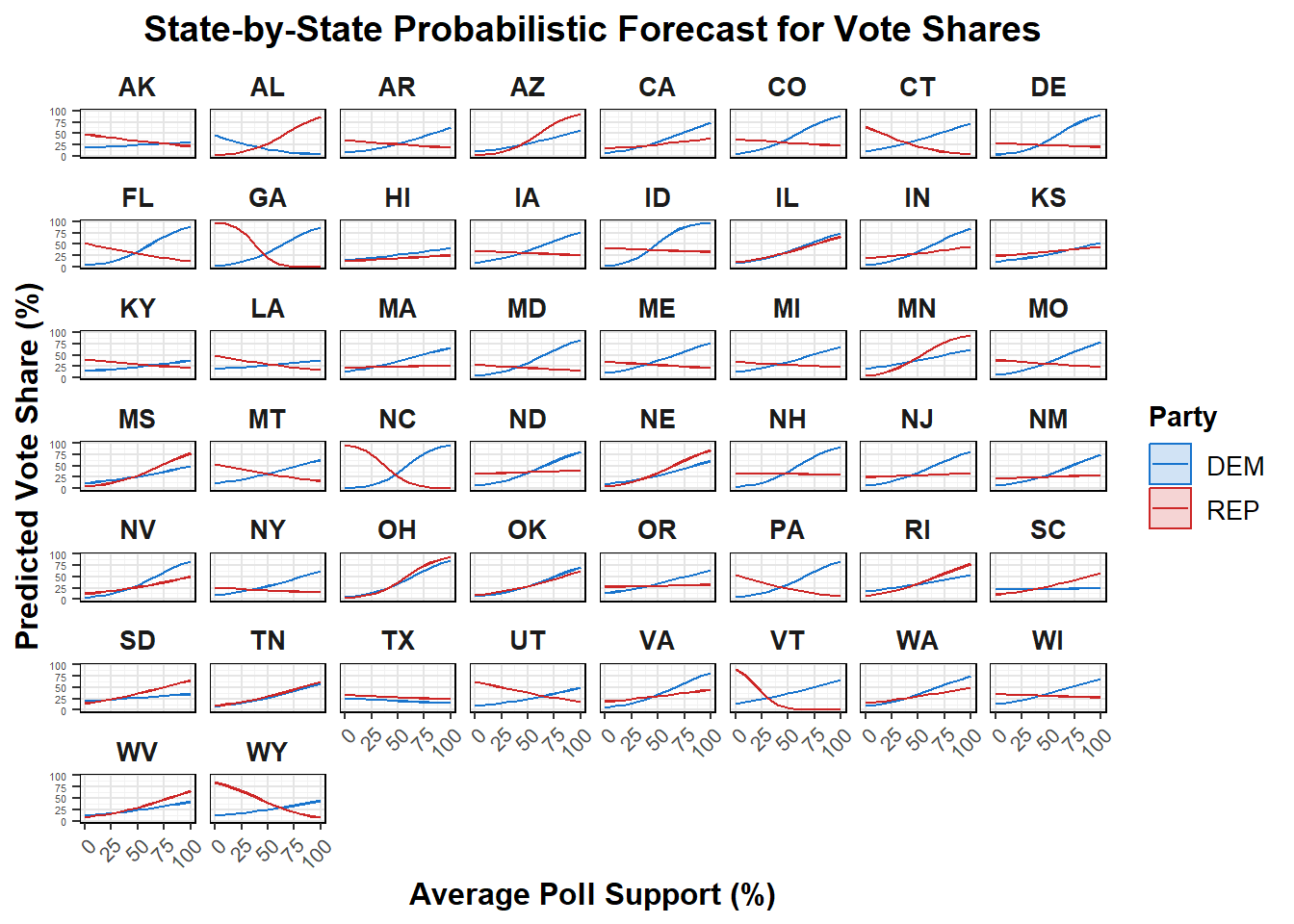
The graphs above show the predicted probabilities of voting for the Democratic and Republican parties as a function of hypothetical average poll support. On the x-axis, the values represent varying levels of public polling support for each party, while the y-axis displays the corresponding predicted vote percentages, expressed as probabilities. As hypothetical poll support increases, the predictions for both parties typically demonstrate distinct trends: for instance, higher poll support generally correlates with an increased likelihood of receiving votes, reflecting the intuitive relationship between public opinion and electoral success. This depends on the state and appears to perform worse in some states that the poll support only model. The confidence intervals shaded around each prediction, which are hard to see, highlight the uncertainty associated with these estimates. Overall, the graphs effectively convey how shifts in poll support can significantly influence voter behavior.
The underlying model code generates probabilistic state forecasts by employing logistic regression to analyze the relationship between voter support and various predictors. Specifically, separate models are created for Democratic and Republican candidates for each state, utilizing the glm() function with a binomial family to model the votes received as a function of predictors. The primary predictor of interest is poll_support, which reflects the percentage of respondents favoring each party in recent polls. Additionally, the models incorporate several other variables that the original did not: latest_pollav_REP and mean_pollav_REP represent the most recent and average polling support for the Republican party, respectively, while GDP_growth_quarterly and RDPI_growth_quarterly capture economic indicators that may influence voter preferences. By iterating over a range of hypothetical poll support values, the code predicts the likelihood of voter support for each party, allowing for a comprehensive understanding of how changes in polling influence electoral outcomes across different states.
It is concerning how differently the model with the additional variables performs, and will need to be explored in the future. From each of these models, I would run simulations based on voter eligible population predictions and the logistic regression to find 2024 results.
## # A tibble: 7,732 × 60
## # Groups: state [50]
## year state D_pv R_pv D_pv2p R_pv2p votes_D votes_R total_votes
## <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 2 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 3 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 4 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 5 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 6 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 7 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 8 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 9 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## 10 1972 California 41.5 55.0 43.0 57.0 3475847 4602096 8367862
## # ℹ 7,722 more rows
## # ℹ 51 more variables: two_party_votes <dbl>, D_pv_lag1 <dbl>, R_pv_lag1 <dbl>,
## # D_pv2p_lag1 <dbl>, R_pv2p_lag1 <dbl>, D_pv_lag2 <dbl>, R_pv_lag2 <dbl>,
## # D_pv2p_lag2 <dbl>, R_pv2p_lag2 <dbl>, weeks_left <dbl>, days_left <dbl>,
## # party <chr>, candidate <chr>, poll_date <date>, poll_support <dbl>,
## # before_convention <lgl>, state_abb <chr>, vep_turnout <chr>,
## # vep_highest_office <chr>, vap_highest_office <chr>, total_ballots <dbl>, …
From this, we see that this model is having a difficult time overall, with Mean Squared Error for Democrats: 661.399 Mean Squared Error for Republicans: 426.1851
I can also use 5 fold cross validation to evaluate this model
## Fold MSE_D MSE_R
## 1 1 450.5822 606.7671
## 2 2 450.0231 610.8412
## 3 3 453.0353 607.8425
## 4 4 453.6386 610.1295
## 5 5 456.9026 608.4865## Mean MSE for Democrats across folds: 452.8364## Mean MSE for Republicans across folds: 608.8133The mean Mean Squared Error (MSE) for the Democratic model across five folds of cross-validation is 454.46, indicating that the model’s predictions for Democratic vote shares deviate from actual values by this amount (squared). In contrast, the Republican model’s average MSE is higher at 608.07, suggesting less accuracy in predicting Republican vote shares. Fold-wise MSE results show that the Democratic model performs consistently across folds, ranging from 449.03 to 460.15, while the Republican model’s MSE ranges from 604.37 to 613.85, indicating stable yet less effective performance. Overall, the results suggest that while both models exhibit relatively low error rates, there is room for improvement, particularly for the Republican model, potentially through further tuning or the exploration of additional features.
Evaluating the Fit of Binomial and Linear Regression Models
Using a linear regression model with the same variables could provide several advantages in predicting electoral outcomes. Firstly, linear regression assumes a direct linear relationship between the predictors and the response variable, which can simplify the interpretation of results and provide clear insights into the influence of each variable. It has been discussed that simpler, linear regression type models perform better in election prediction. Moreover, linear regression is less complex than generalized models, making it less prone to overfitting, particularly with smaller datasets like election results data. By adopting linear regression, we may achieve a model that is easier to understand and communicate, while still accurately capturing the dynamics of voter behavior and electoral outcomes.
Prediction
I will use the updated binomial in each of my seven states of interest to determine how my prediction for this week may have changed from the last.
Pennsylvania
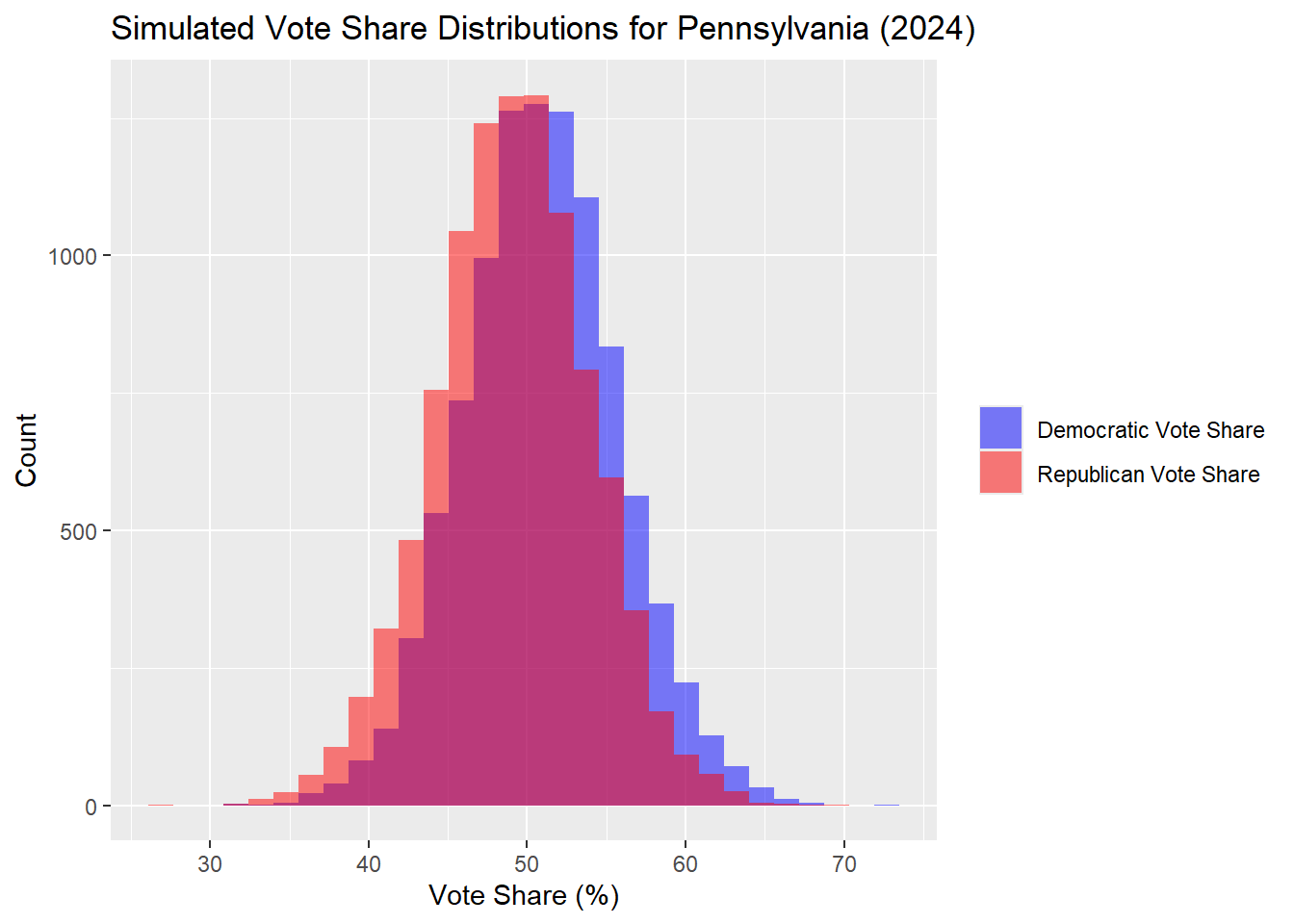
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -14.14 |
| 50% | Median | -1.79 |
| 90% | 90th Percentile | 10.58 |
Looking at the state of Pennsylvania, our model predicts 50.86% Harris to 49.14% Trump. This result is closer than last week, which had a Democrat popular vote share of 51.75% and Republican of 48.25%.
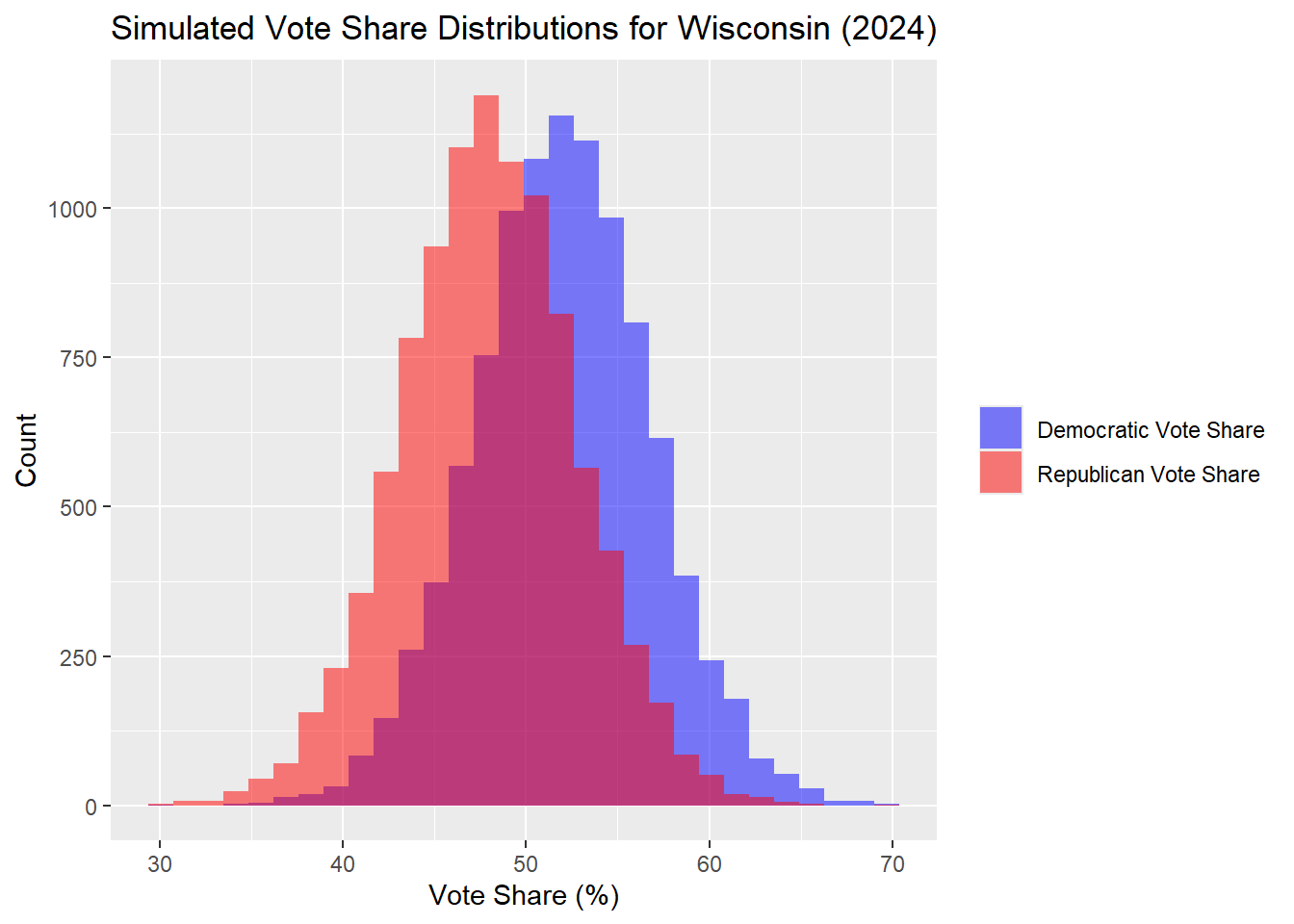
Wisconsin
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -16.02 |
| 50% | Median | -4.08 |
| 90% | 90th Percentile | 8.13 |
These are the exact slightly closer results than last week’s binomial model, with Harris 51.97% and Trump 48.03%.
North Carolina

| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -8.73 |
| 50% | Median | 6.58 |
| 90% | 90th Percentile | 21.06 |
In the North Carolina outcomes, the median simulated outcome was a Democrat popular vote share was 46.79% and Republican 53.21%, with a slight but likely statistically insignificant increase on the democratic side of 0.18pp.
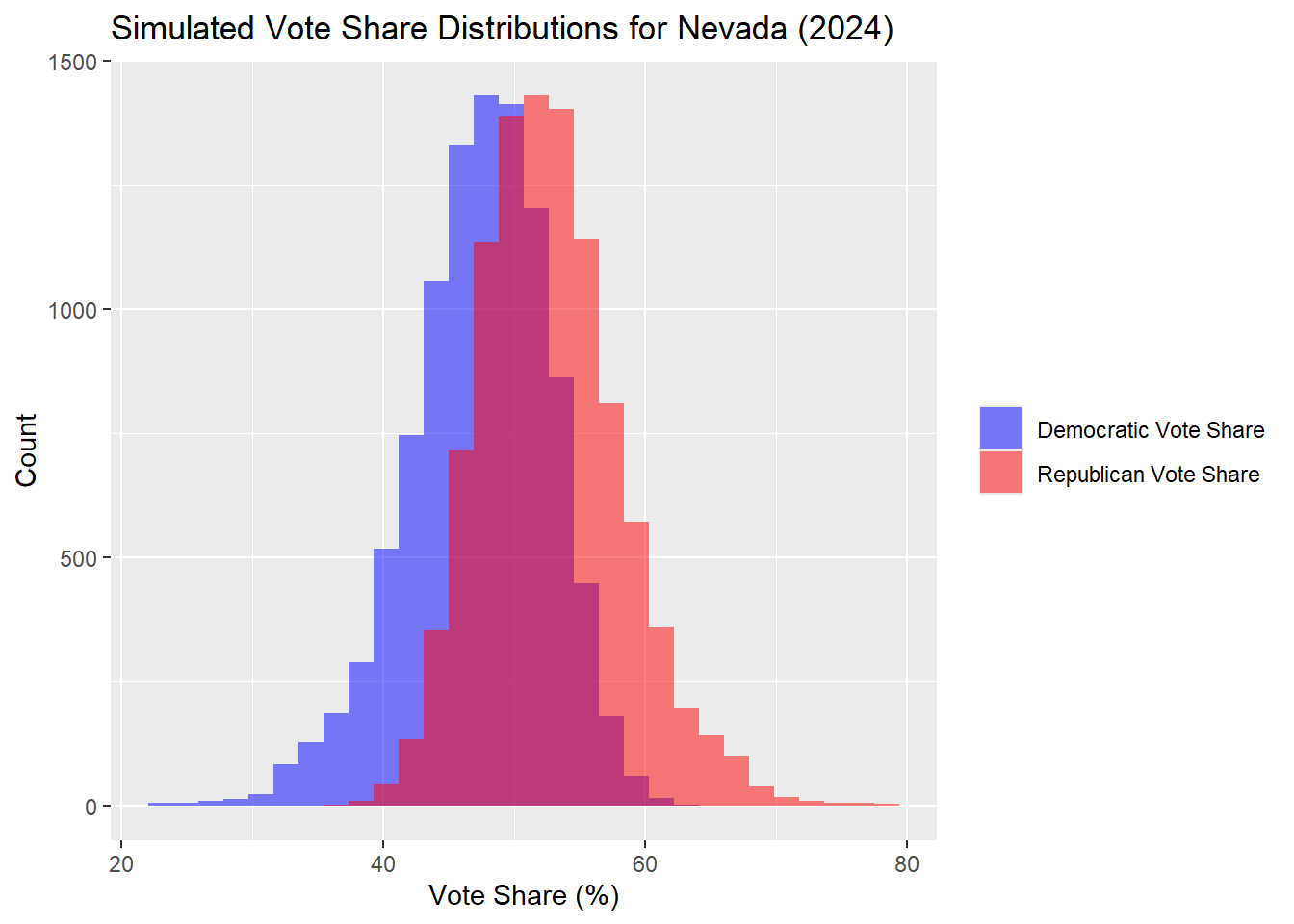
Nevada
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -7.46 |
| 50% | Median | 4.69 |
| 90% | 90th Percentile | 19.56 |
Nevada has gotten slightly less close according to these new predictions, 47.58% Harris to 52.42% Trump, but likely an insignificant change from last week. Trump still wins this state.
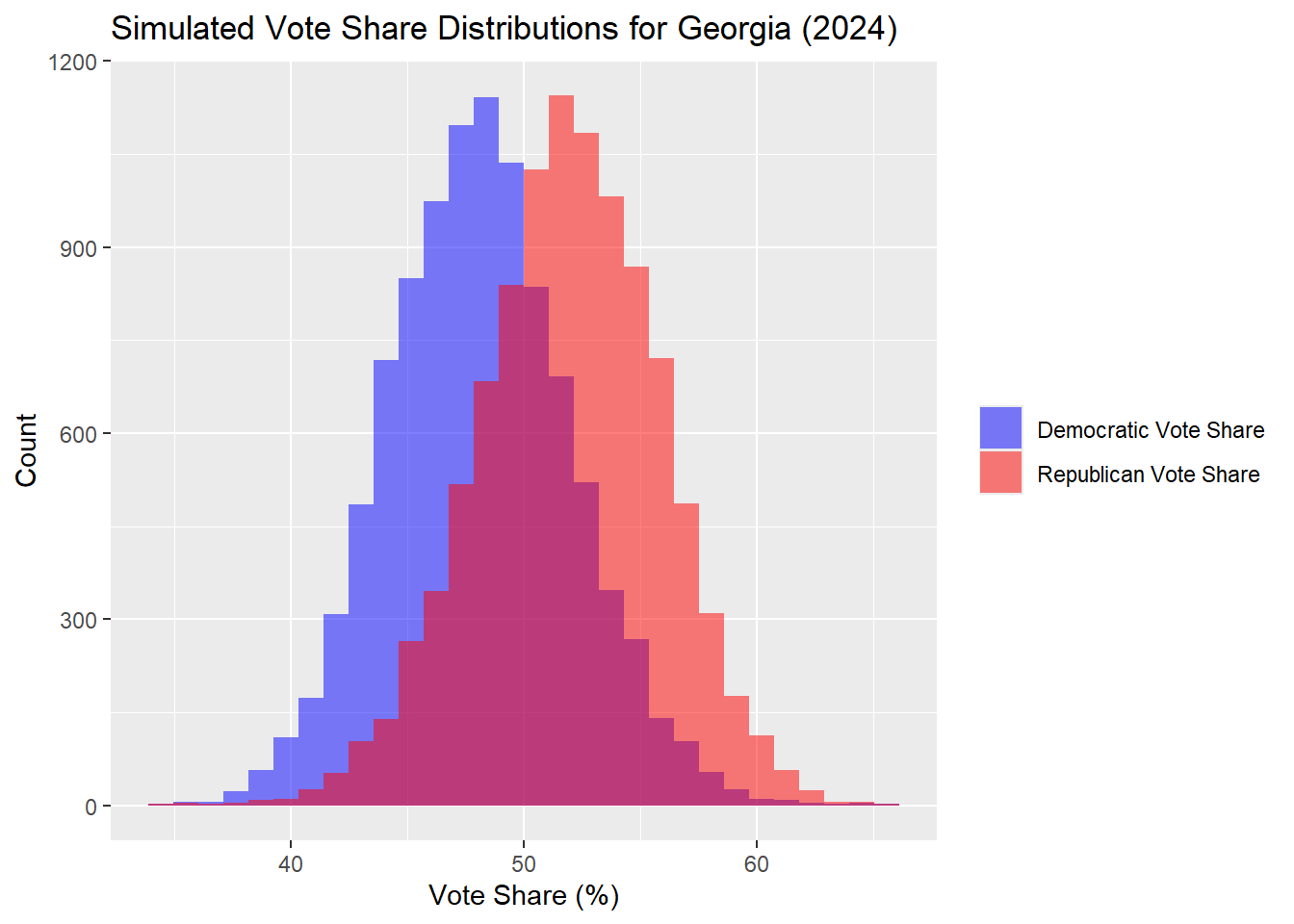
Georgia
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -6.25 |
| 50% | Median | 4.00 |
| 90% | 90th Percentile | 13.56 |
The results in Georgia lead to Harris 47.92% to Trump 52.08%, consistent with the results from the past week. These numbers are slightly closer.
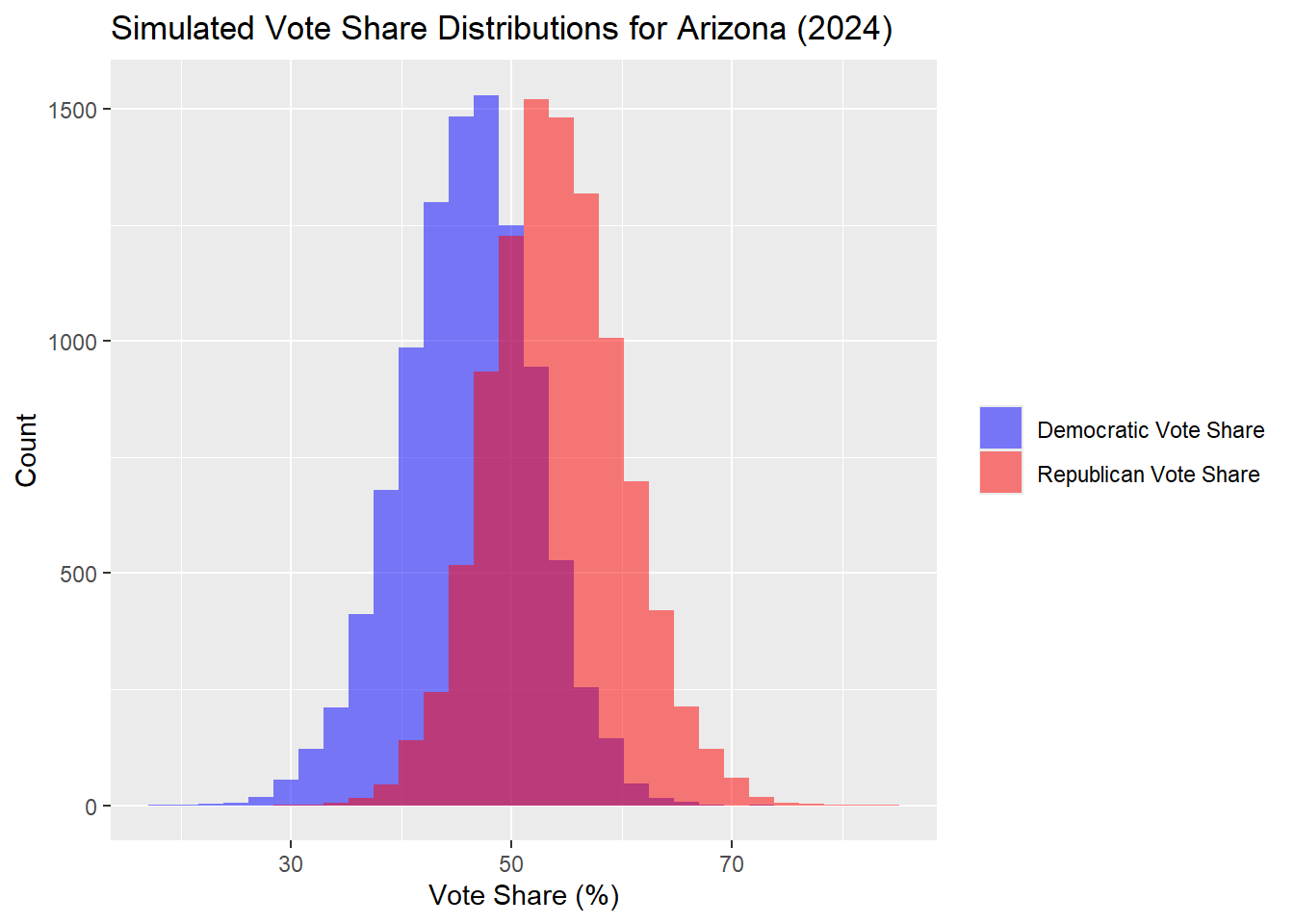
Arizona
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -6.72 |
| 50% | Median | 7.70 |
| 90% | 90th Percentile | 23.72 |
The Arizona results are more extreme in the Republican direction this week, with more than a two point change in the margin in the prediction, likely due to recent polling. Harris is predicted 45.99% to Trump’s 54.01%.
Michigan
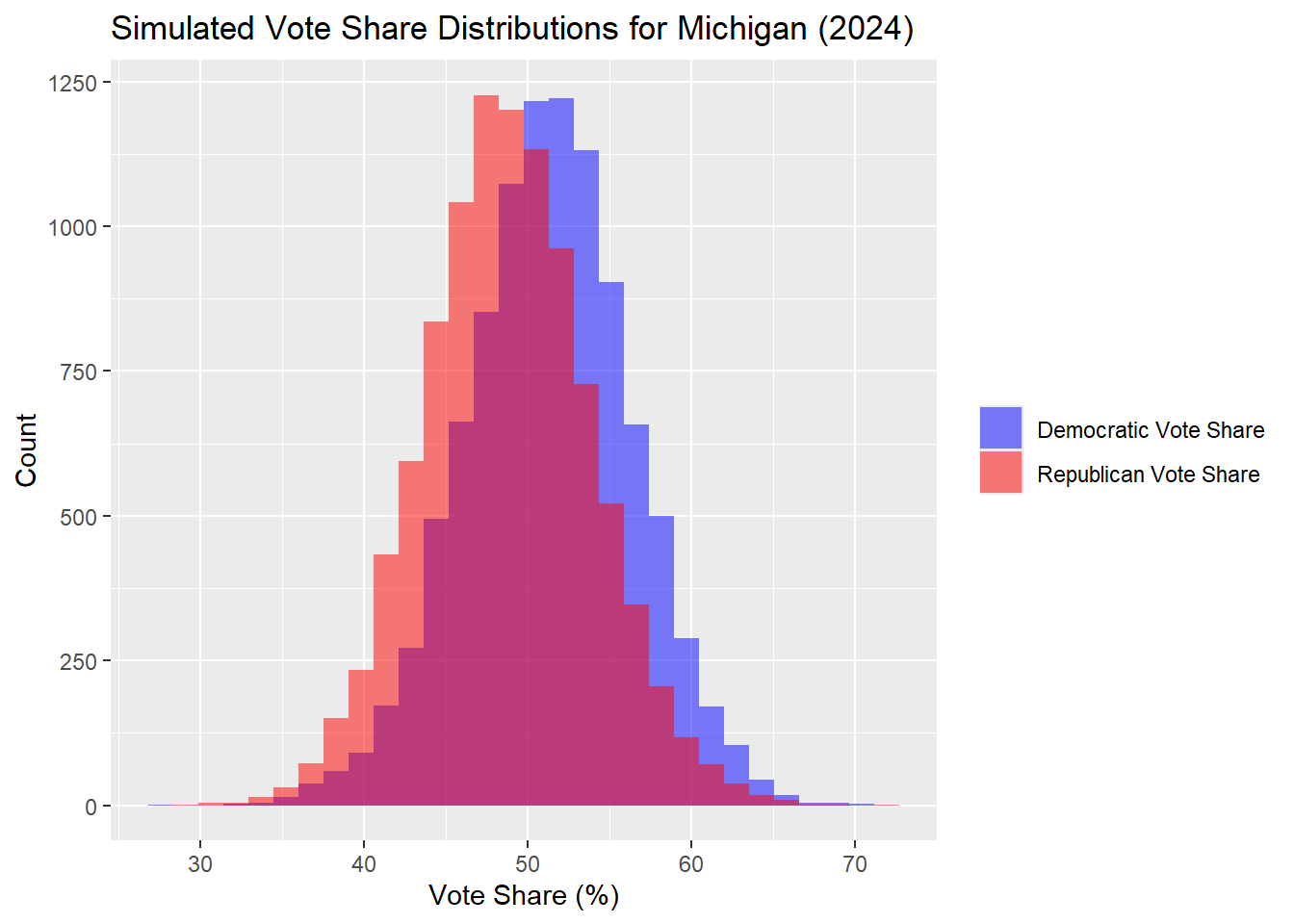
| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -15.45 |
| 50% | Median | -2.69 |
| 90% | 90th Percentile | 10.39 |
These results are nearly identical to the simulations of the Michigan results last week, with a median popular vote for Harris of 51.34% and Trump of 48.66%
With no state level prediction changes, I am left with the result of
Wisconsin: D
Pennsylvania: D
North Carolina: R
Nevada: R
Georgia: R
Arizona: R
Michigan: D
Culminating in Harris 270 - Trump 268.
Data Sources
- Popular Vote Data, national and by state, 1948–2020
- Electoral College Distribution, national, 1948–2024
- Demographics Data, by state
- Primary Turnout Data, national and by state, 1789–2020
- Polling Data, National & State, 1968–2024
- FRED Economic Data, national, 1927-2024
- ANES Data, national
- Voter File Data, by state