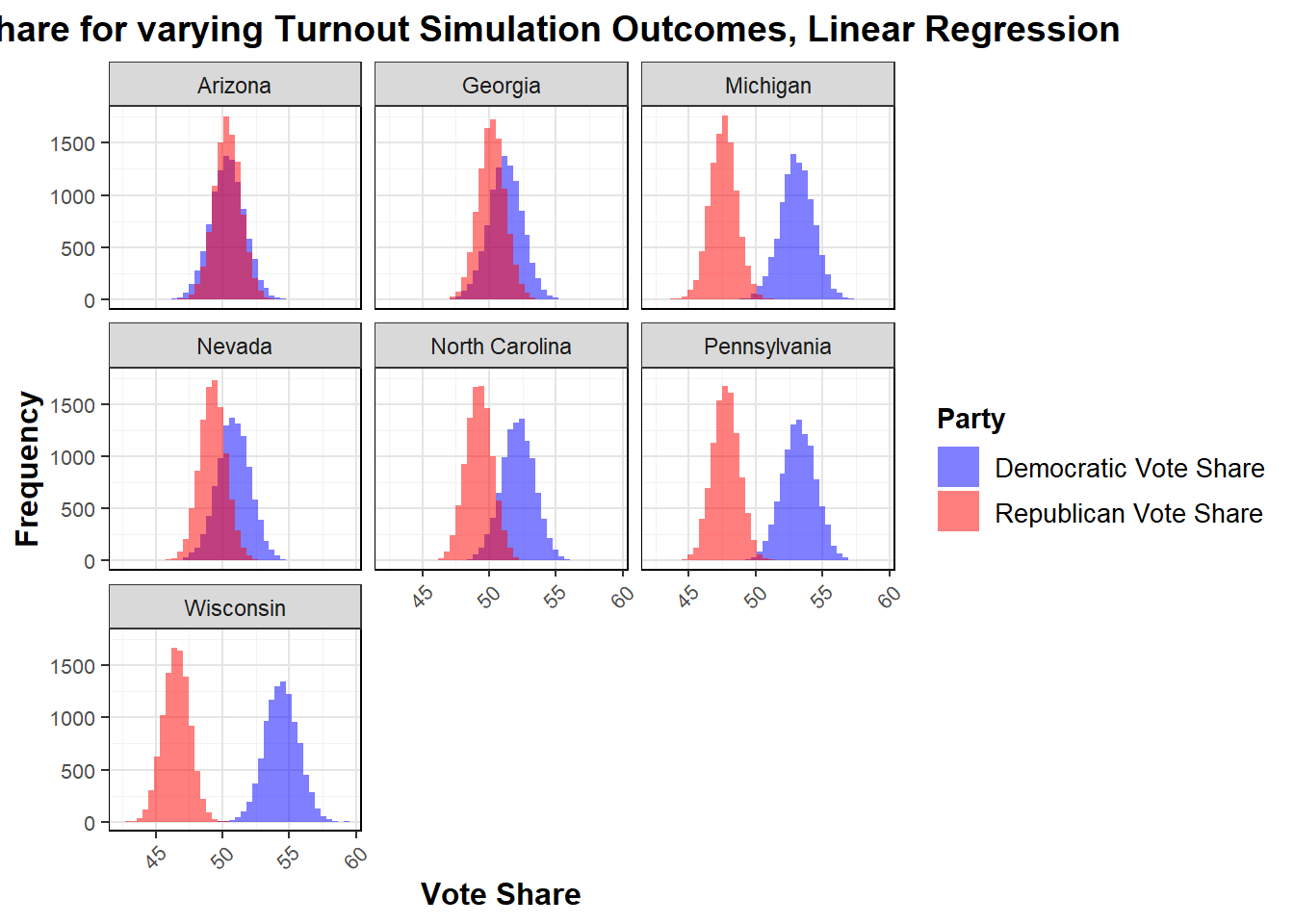
This post marks the end of my weekly blog predicting the 2024 presidential election results for Gov 1347: Election Analytics, Fall 2024, at Harvard College. Thank you for sticking with me for the past nine weeks as we have explored the ins and outs of campaigns, fundamental variables, and model specifications used in predictive modeling of elections.
Nine weeks ago I presented a simple model to predict the outcome of the election– \(vote_{2024} = 0.75 \cdot vote_{2020} + 0.25 \cdot vote_{2016}\). While this simple weighted average may seem to over-simply the complex process that is the presidential election, as discussed over the past blog posts it is incredibly important to carefully evaluate all elements of a model. The most complicated model may not always be the best, as parsimony can be key and overfitting can be fatal.
Though the results of the election to evaluate with my final model presented below may not be announced for weeks, I nevertheless present a full picture of how the results, whether they arrive in two or sixteen days, could look, as well as the means to evaluate which predictors ended up having the most impact. In the following sections, I will bring you through my final model, noting why I made each decision and building upon the past nine weeks of work and blog posts to present a final picture for the election.
A Note on the Binomial Simulations Model
For the past few blog posts, I have focused on a logistic regression model and using binomial simulations to predict the results. Unfortunately, this model broke down one day before the election as I attempted to make important changes I felt necessary to have a more accurate model. While it may be worth going back to see in retrospect how this model may have done, as I move forward I will keep in mind it’s prediction: Harris 270 to Trump 268, splitting the battleground states with NC, NV, AZ, and GA to Trump and PA, WI, and MI to Harris. While my replacement model does not have the same prediction as this, it is worth keeping at the back of our minds.
However, not all is lost. This change allowed me to re-explore the linear regression model, a much simpler but also proven effective method at predicting popular vote and vote margin, as I carry out below. The ability to return to an OLS model with multiple predictors (as discussed later, this may be pushing it with overfitting) has opened up new avenues of exploration and new considerations in my model. OLS also allowed for much easier interpretability as I communicate my results to you below, as the logistic model based on hypothetical poll support was not directly clear to the observer. OLS models produce coefficients that directly relate to changes in the predicted vote share, as we will see below.
Linear Model Formulation
There are three linear models used in this final blog post. One predicts Democratic two-party popular vote, one Republican two-party popular vote, and the third the vote margin. While I have provided the specifications for all three below, it is the vote margin model that I will use to make my prediction, as will be discussed below as we dive into each model. The vote margin allows us to handle the infinite bounds of a linear regression better within the context of election results as percentages.
The specifications for the two-party popular vote models, which are used as motivating examples for the margin model, are below:
\[ D_{\text{pv2p}} = \beta_0 + \beta_1 \cdot D_{\text{pv2p_lag1}} + \beta_2 \cdot D_{\text{pv2p_lag2}} + \beta_3 \cdot \text{latest_pollav_DEM} + \beta_4 \cdot \text{mean_pollav_DEM} \] \[ + \beta_5 \cdot \text{vep_turnout} + \beta_6 \cdot \text{GDP_growth_quarterly} + \beta_7 \cdot \text{RDPI_growth_quarterly} \] \[ + \beta_8 \cdot \text{GDP_growth_quarterly} \cdot \text{incumbency} + \beta_9 \cdot \text{RDPI_growth_quarterly} \cdot \text{incumbency} + \epsilon \]
\[ R_{\text{pv2p}} = \alpha_0 + \alpha_1 \cdot R_{\text{pv2p_lag1}} + \alpha_2 \cdot R_{\text{pv2p_lag2}} + \alpha_3 \cdot \text{latest_pollav_REP} + \alpha_4 \cdot \text{mean_pollav_REP} \] \[ + \alpha_5 \cdot \text{vep_turnout} + \alpha_6 \cdot \text{GDP_growth_quarterly} + \alpha_7 \cdot \text{RDPI_growth_quarterly} \] \[ + \alpha_8 \cdot \text{GDP_growth_quarterly} \cdot \text{incumbency} + \alpha_9 \cdot \text{RDPI_growth_quarterly} \cdot \text{incumbency} + \epsilon \]
Each of the beta and alpha coefficients, as well as justification for the inclusion and exclusion of each variable, are provided in the following sections. It is worth noting that the predictors including in these model have been carried through nearly the same each of the past few weeks with me as I make small adjustments to find the most effective set of predictors across models. Had the logistic model/ binomial simulations model been able to be carried to completion, I would have ensembled it with the linear and elastic net regressions using super learning, such that all three models would use the same predictors. This indicates my desire to adjust for the potential error in any one model specification by weighing across results. The binomial model was much more Republican leaning than my linear model shown here today, and more in line with the current predictions from organizations like 538.
Moving on the the margin model, I chose to focus on vote margin. Predicting vote margin rather than vote share simplifies the model by focusing on the difference between candidates, which is often more stable. It directly captures the competitive gap while keeping predictions naturally bounded and easy to scale 0-100%. This approach leads to the linear regression model of:
\[ \text{margin (D-R)} = \beta_0 + \beta_1 \cdot \text{margin_lag1} + \beta_2 \cdot \text{margin_lag2} + \beta_3 \cdot \text{latest_pollav_DEM} + \beta_4 \cdot \text{mean_pollav_DEM} + \beta_5 \cdot \text{latest_pollav_REP} \] \[ + \beta_6 \cdot \text{mean_pollav_REP} + \beta_7 \cdot \text{vep_turnout} + \beta_8 \cdot \text{GDP_growth_quarterly} + \beta_9 \cdot \text{RDPI_growth_quarterly} \] \[ + \beta_{10} \cdot \text{GDP_growth_quarterly} \cdot \text{incumbency} + \beta_{11} \cdot \text{RDPI_growth_quarterly} \cdot \text{incumbency} + \epsilon \]
Linear Model Variables
I will now go through each variable, which model(s) it is included in, and why it is included. The variables have also been reviewed each week in my blog posts, so their inclusion is the culmination of statistically significant performance and good model evaluation results.
Lagged Popular Vote Share: This include R_pv2p_lag1, D_pv2p_lag1, R_pv2p_lag2, and D_pv2p_lag2. These are lagged vote shares of the past two election cycles before the current year you are considering. Since the first week, lagged vote share has been shown to have strong predictive power in both simple and more complex models, leading to statistically significant coefficients. Past voting behavior is a good indicator of the future, and although it may not be exact, this can be seen by looking at states over time, as we did in weeks one and two. States do not simply flip from 70% D one year to 60% R then next and back to 80% D, they stay relatively the same in who they vote for in aggregate, and therefore lagged vote share is important to include. I use two-party popular vote share in particular as to abstract away the influence of third party candidates or other flukes which may not be relevant this late in the election cycle. These are used in the two popular vote models, and are split by party.
Latest and Mean Poll Averages: The latest poll average looks at the average of the polls in the most recent day available, using polls included by 538 in their aggregation. It is important to note that 538 has been noted as potentially missing some up-and-coming young pollsters whose results will therefore not be considered in this model. I considered and tested using both a 1 day and 3 day rolling average of the poll support, as well as a variety of other weighting schemes, but latest poll average has been performing the best in model evaluation, likely due to how close to the election it is. As explored in the past, whether polling or economic fundamentals matter more closer to the election has been debated, so I have taken the route of not up or down weighting either. Also including for polling is the mean polling average over the last 30 weeks of the cycle. The decision of whether or not to include the data pre-candidate switch was a tough one, but as much attention has been payed to Harris as the current VP, important member of the administration, and tying her to Joe Biden, I thought his approval could be a proxy to hers if she had been announced earlier (despite the limited party support for her and moves to even replace her on the ticket pre-candidate switch). This is the counterfactual world in which my model must sit. These are split by party and used in all three regressions. In the margin model, I chose to use Democratic poll numbers because my margin was defined by Democrats minus Republicans. In the future, I would like to explore using margins in the polling averages as well.
Turnout: Though in week five we saw the very minimal impact of demographics and specific turnout in our models, out of principle I decided to include it. While the literature review in the week 5 blog post pointed out the limited ability to predict turnout from other demographics, I do believe that large changes in turnout can change outcomes, but if and how these can happen does not seem plausible to me. Because of this, I created a turnout Ridge regression lagged turnout model, but its weights were throw off by the small amount of data and issues with 2020 and COVID, and I later used turnout as a means to do simulations on different numbers of people from the voter eligible population turning out on election day. As noted in previous weeks, a separate turnout prediction model can be important, as studies like Enos and Fowler (2016) suggest that ground efforts can increase turnout by as much as 6-7% in heavily targeted areas. For this reason, I recognize its importance of predicting turnout, especially in the final week of the campaign.
Quarterly Economic Variables: As noted in week two, economic fundamentals are incredibly strong at predicting election outcomes, particularly when interacted with an incumbency indicator. From week 2, I found that short term economic outcomes have much more significant impact on people’s decisions than do long term. Additionally, people are sociotropic in their view of the economy, meaning they base their choices on national economic conditions affecting others. This aligns with findings on the importance of national over state economic conditions. As such, I have used short term (quarter 2) economic indicators at the national rather than state level. Because the economy reflects more strongly on incumbents, I also have an interaction term between each of the economic indicators and an incumbency variable, which is coded to weigh the impact of the economy more strongly into their prediction than the other party. Additionally, given that incumbent candidates matter much more than incumbent parties, I have tried to take this into account when considering who counts as an incumbent. For this election, I have deemed that Harris is the incumbent, although she is only the head of the party in charge, not the president. In the future, I would want to readjust this weight to also include whether the party or person had previously been in office as a weighted indicator with simple candidate incumbency. These are used in all three regression models.
Lagged Margins: As with lagged vote share, for the margins model lagged margins can be calculate for the two previous election cycles. The model specifications above show how I replaced the lagged vote share with this value to better specify my margins model.
The Margin Model: Coefficients and Interpretation
We were introduced to the margins model above as
\[ \text{margin (D-R)} = \beta_0 + \beta_1 * \text{margin_lag1} + \beta_2 * \text{margin_lag2} + \beta_3 * \text{latest_pollav_DEM} + \beta_4 * \text{mean_pollav_DEM} + \beta_5 * \text{latest_pollav_REP} \] \[ + \beta_6 * \text{mean_pollav_REP} + \beta_7 * \text{vep_turnout} + \beta_8 * \text{GDP_growth_quarterly} + \beta_9 * \text{RDPI_growth_quarterly} \] \[ + \beta_10 * \text{GDP_growth_quarterly} * \text{incumbency}} + \beta_11 * \text{RDPI_growth_quarterly} * \text{incumbency} + \epsilon \] The variables included in this model, as described above, were found to be statistically significant in the past nine weeks of evaluation. As a result of my last minute model switch, this is the first iteration of the margins linear regression model. I first calculate lagged margins for use, as I will be predicting D-R margins. I chose to use the incumbency interactions for democrats in this case so their signs would line up with the direction of the margin subtraction. This is once again a pooled model for the swing states, as discussed above.
First, I specify the the model’s coefficients
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -21.9275406 | 12.5266122 | -1.7504765 | 0.0885552 |
| margin_lag1 | 0.1611392 | 0.0983592 | 1.6382723 | 0.1100772 |
| margin_lag2 | -0.0991325 | 0.1189715 | -0.8332461 | 0.4102004 |
| latest_pollav_DEM | 1.2609204 | 0.4565342 | 2.7619406 | 0.0089897 |
| mean_pollav_DEM | -0.0940902 | 0.2646677 | -0.3555033 | 0.7242872 |
| latest_pollav_REP | -0.6511034 | 0.3381705 | -1.9253700 | 0.0621113 |
| mean_pollav_REP | -0.3213266 | 0.3022814 | -1.0630048 | 0.2948587 |
| vep_turnout | 17.5123591 | 12.9928359 | 1.3478473 | 0.1861286 |
| GDP_growth_quarterly | 0.4041927 | 0.3571323 | 1.1317732 | 0.2652126 |
| RDPI_growth_quarterly | 0.2203304 | 0.3510069 | 0.6277096 | 0.5341559 |
| GDP_growth_dem_weighted | 0.0124165 | 0.3278230 | 0.0378756 | 0.9699961 |
| RDPI_growth_dem_weighted | -0.0463084 | 0.3618189 | -0.1279878 | 0.8988709 |
The linear regression results for the vote share margin model highlight important factors influencing Democratic and Republican margins. The intercept of -21.93 suggests a baseline Republican advantage, but its significance is marginal (p = 0.088). This would be interesting to explore in more detail. The latest Democratic polling average is significant (p = 0.009), indicating that a one-point increase in polling raises the margin by 1.26 points, underscoring the importance of current polls as this is a huge jump that could turn many of the states when we get to the simulations. Conversely, the latest Republican polling average shows a negative impact of -0.65pp on the margin (p = 0.062), suggesting stronger Republican polls can decrease the Democratic margin, which is expected. Note that this is significant at the 10% level only while the Democratic polls are significant at the 1% level. While voter turnout has a substantial coefficient of 17.51, its significance is low (p = 0.186), which contrasts with what we saw in the individual two-party popular vote models. Overall, current polling data plays a critical role in shaping vote margins because we are so close to the election, while lagged effects and economic factors appear less influential, which is consistent with one of the two approaches to weighing results closer to the election. While I will not be doing any weighting of this sort based on how close we are to election day in my final prediction, see Week 2 for more information.
The Margin Model: Simulations and Uncertainty
Now that the model has been specified, I will move on to using simulations varying the voting eligible population again to get a sense of the predicted two-way popular vote margin from this model. It is important to note that this also could be done by varying the polling averages within their standard deviations, which would result in more variability due to their larger significance and coefficients. Either way, the simulations result in some starkly different results than past models like the binomial, as we see states which are fully predicted for Harris.
| State | Lower Bound | Mean Margin | Upper Bound | Winning Party |
|---|---|---|---|---|
| Arizona | -2.4176448 | -0.6899017 | 1.037842 | Republican |
| Georgia | -1.6725299 | 0.0448436 | 1.762217 | Democrat |
| Michigan | 1.4074161 | 3.1388499 | 4.870284 | Democrat |
| Nevada | -0.9506591 | 0.7659417 | 2.482543 | Democrat |
| North Carolina | -1.0068164 | 0.7190907 | 2.444998 | Democrat |
| Pennsylvania | 0.7983981 | 2.5309086 | 4.263419 | Democrat |
| Wisconsin | 2.3254737 | 4.0154125 | 5.705351 | Democrat |
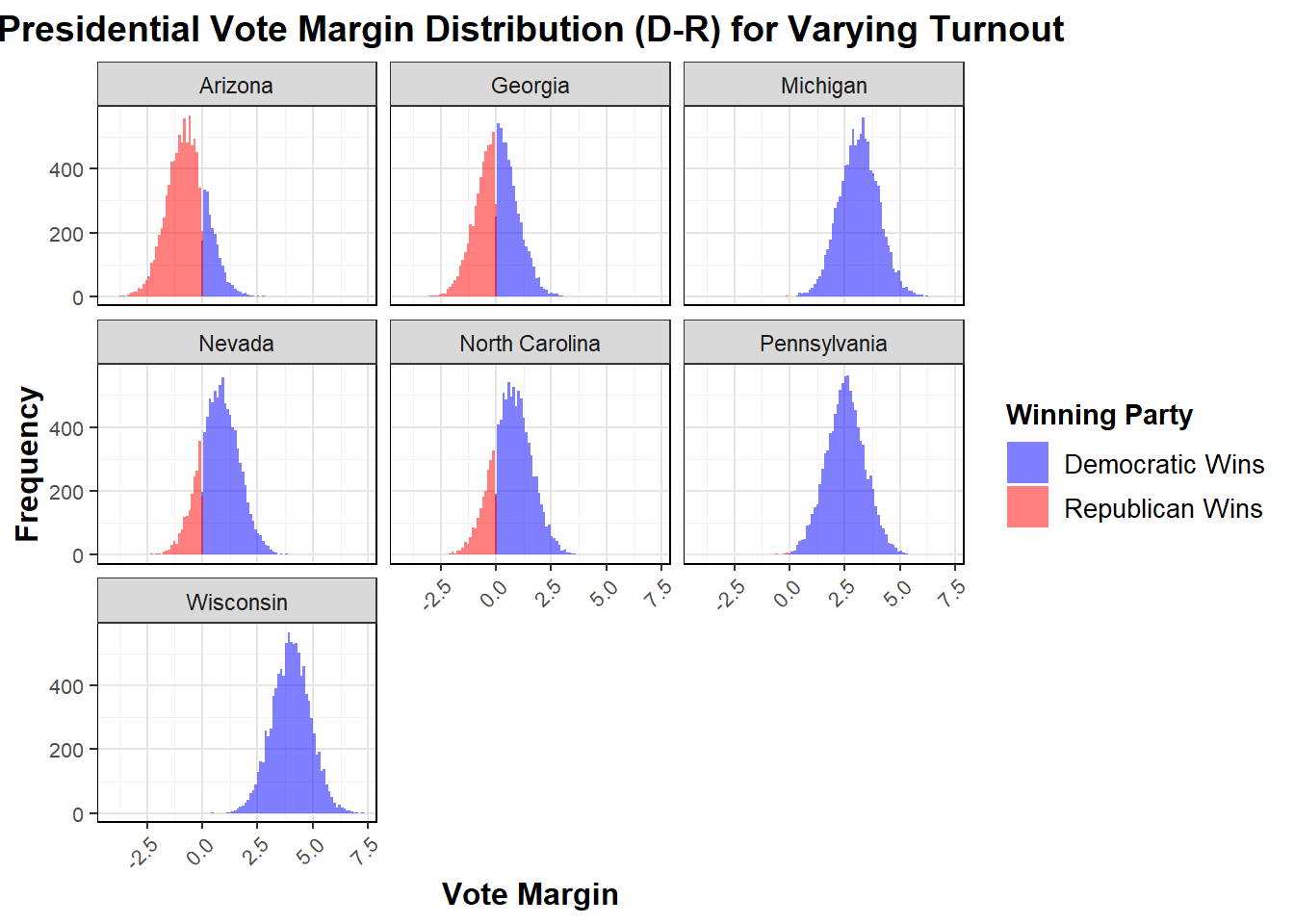
I am skeptical that the vote margins in some of these swing states are so in favor of Harris, but given the impact of voting eligible population turnout in the model it may not be surprising. Additionally, it gives us an opportunity to think about how to approach uncertainty in this model as I attempt to take the predicted vote margins and convert them to Democratic and Republican vote share using a \(50 + margin/2\) shift. To handle uncertainty, I have decided to provide predictive intervals, which are explained in more detail below, alongside my predictions for these based on the simulations.
| State | Lower Bound (Margin) | Mean Margin | Upper Bound (Margin) | Lower Bound (D) | Mean Democratic Vote | Upper Bound (D) | Lower Bound (R) | Mean Republican Vote | Upper Bound (R) | Winning Party |
|---|---|---|---|---|---|---|---|---|---|---|
| Arizona | -8.31 | -0.69 | 6.93 | 42.18 | 49.66 | 57.13 | 42.87 | 50.34 | 57.82 | Republican |
| Georgia | -7.57 | 0.04 | 7.66 | 42.55 | 50.02 | 57.49 | 42.51 | 49.98 | 57.45 | Democrat |
| Michigan | -4.48 | 3.14 | 10.76 | 44.10 | 51.57 | 59.04 | 40.96 | 48.43 | 55.90 | Democrat |
| Nevada | -6.85 | 0.77 | 8.38 | 42.91 | 50.38 | 57.85 | 42.15 | 49.62 | 57.09 | Democrat |
| North Carolina | -6.90 | 0.72 | 8.34 | 42.89 | 50.36 | 57.83 | 42.17 | 49.64 | 57.11 | Democrat |
| Pennsylvania | -5.09 | 2.53 | 10.15 | 43.79 | 51.27 | 58.74 | 41.26 | 48.73 | 56.21 | Democrat |
| Wisconsin | -3.60 | 4.02 | 11.63 | 44.54 | 52.01 | 59.48 | 40.52 | 47.99 | 55.46 | Democrat |
Based on this results table, The mean vote shares and mean margin allow me to call each state such that Harris takes all of the swing states except for Arizona, which goes to the Republicans. However, these means without context are extremely deceiving, as looking at the prediction interval around them one can see that all races are well within the margin of error of the 95% predictive interval. In particular, in Georgia, the Democrats only lead in the simulation by 0.04 percentage points, a tiny margin compared to something like Wisconsin’s 4.02 percentage point lead for Harris. There is still a clear chance for both candidates in all states.
I used a predictive instead of confidence interval above because it provides a more realistic range for individual state-level outcomes, accounting for both model uncertainty and inherent variability in the data. Unlike a confidence interval, which only reflects uncertainty around the mean prediction, a predictive interval captures the total variability you expect in an actual election result for each state. This added variability (in the residuals) is essential here because we want the possible outcomes of single events rather than in estimating an average across many possible elections.
Residual variation is the difference between observed outcomes and those predicted by my margin model. They are random noise or unpredictable factors affecting the outcome that aren’t included in the model, which makes me feel more comfortable with my predictions and uncertainty around them. By incorporating this residual variation into the predictive interval, I acknowledge that even if I know the model’s general trend, individual outcomes may differ from that trend due to factors not captured by the model, which is a part of election forecasting we have been discussing in class for the past nine weeks. As such, predictive intervals provide a more comprehensive and realistic assessment of the uncertainty around individual state margins, better reflecting the complexities of real-world electoral outcomes.
The Margin Model: Model Evaluation
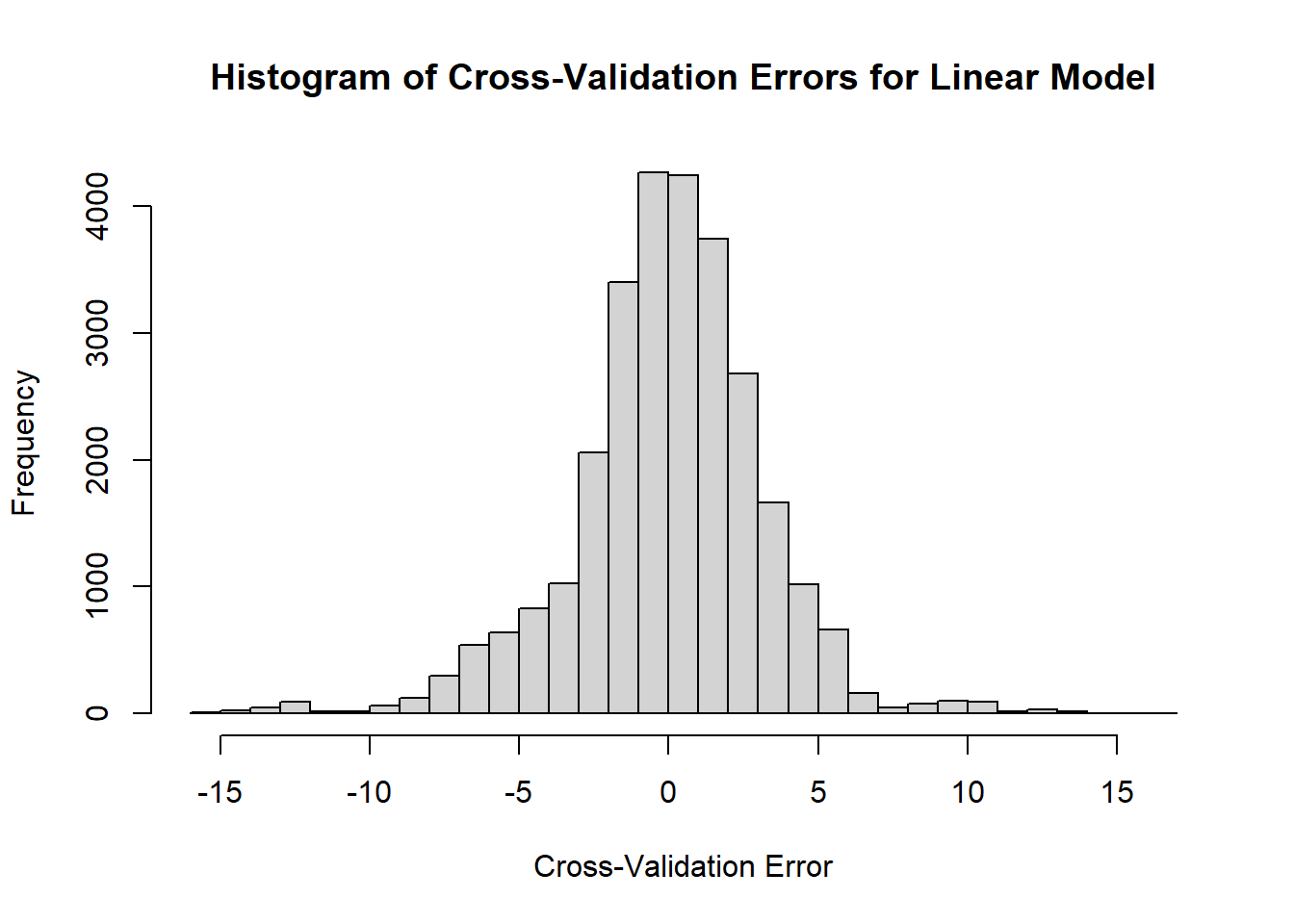
As before, I will evaluate my linear regression model using 10-fold cross validation. 10-fold cross-validation divides the dataset into ten subsets, trains the model on nine of these subsets while testing it on the remaining subset, and then repeats this process ten times to ensure that every subset has been used for testing, which help estimate the model’s generalizability. I also perform cross-validation by randomly sampling 20% of a dataset for out-of-sample testing 1,000 times, refitting a linear regression model on the training data, predicting the margins on the test set, and then calculating the prediction errors to evaluate the model’s performance. The results of these two can be seen below:
| Metric | Margin In-Sample | Margin Out-Of-Sample |
|---|---|---|
| R-squared | 0.9147461 | 0.8866863 |
| RMSE | 3.2789197 | 3.8909490 |
| Metric | Value |
|---|---|
| Mean Absolute Error | 3.464866 |
| Root Mean Squared Error | 4.921101 |
| Standard Deviation of Errors | 4.921041 |
The evaluation metrics for the margin model show strong performance, with an R-squared of 0.9147 for in-sample and 0.8055 for out-of-sample, indicating the model explains a significant portion of the variance in the training data but has a notable drop in predictive ability on new data, suggesting possible overfitting. The Root Mean Squared Error (RMSE) of 3.279 in-sample versus 4.511 out-of-sample supports this, as the model performs much better on the training data. Also, this model outperforms the previous models split by Democratic and Republican vote shares, suggesting a more effective capture of the dynamics affecting vote margins. Overall, while the model is strong, it is not clear if it will be generalizable enough.
Looking at the result for the 1000 draws, I calculated MAE, MSE, and SD of the errors. The Mean Absolute Error (MAE) of 3.449 indicates that, on average, the model’s predictions deviate from the actual margins by 3.45 percentage points, which is a moderate level of accuracy. The Root Mean Squared Error (RMSE) of 4.898 is higher than the MAE, so as before it is likely that the model has larger prediction errors. The Standard Deviation of Errors of 4.894 indicates variability in the prediction errors, suggesting that while the model may perform well on average, it can produce predictions that vary significantly from the actual margins. Together, these metrics suggest that while the model provides reasonable predictions, there is room for improvement, particularly in reducing larger errors. Due to the limiations in data available for election prediction, this may be difficult to overcome, but I am confident in this model’s ability given these values.
Other Important Decisions
While I had originally specified wanting to use 1964 to present data, due to certain dataset limitations I have had to adjust to 1980. This gives very few elections on which to test and train my model, resulting likely in overfitting as noted above. Given the changing landscape of election laws, I see this as a way to account for legal consistency is that has changed the electorate over time in the data I have, so it has an upside.
Additional decisions I have made include focusing my predictions on state-level outcomes in the seven swing states, which will then be aggregated to predict the overall Electoral College result. These seven states are: Wisconsin, Michigan, Nevada, Arizona, Pennsylvania, Georgia, and North Carolina. This choice came from Week 4, when upon evaluation of expert predictions and their accuracy, I found that the Cooke Political Report and Sabato’s Crystal Ball heavily agreed on states expect for these seven, and upon confirmation with other expert predictions I confirmed that the other could be considered settled. As a result, my predictions only focus on predicting the popular vote in these seven states and then using their predictions to make an electoral college prediction. This final model has led to results in these states of
Wisconsin: D Michigan: D Nevada: D Arizona: R Pennsylvania: D Georgia: D North Carolina: D
The Ensemble That Never Was
As discussed before, the binomial model I had planned to bring forward met a sudden end. My original plan was to combine the presented linear model, an elastic net model, and the binomial model through super learning to get rid of the potential biases inherent in each formulation while using the same predictors, something I don’t usually see in ensembling. This allows the model to balance the benefits of pooled predictions with the more specific insights from multiple models. By using appropriate checks on model performance, ensembling helps create a more accurate and balanced prediction by drawing from multiple perspectives. The combination of pooling and ensembling makes for a powerful approach that can improve the overall robustness of the election forecast. Both ensembling and pooled models were used in the models described in the previous sections describing my work from past weeks.
The bright side is that my model is now much simpler, which accounts for the idea that the simplest models often do best. However, take a grain of salt that my binomial model predicted 270 Harris to 268 Trump, as compared to the below prediction. I believe this 270 to 268 model is more likely to happen.
Final Prediction
As this project draws to a close, I am ready to make my final prediction. Based on the simulations from the two-party vote margin linear regression model, I am ready to predict
308 Harris - 230 Trump Wisconsin: D, 52.01% Michigan: D, 51.58% Nevada: D, 50.39% Arizona: R, 50.34% Pennsylvania: D, 51.26% Georgia: D, 50.02% North Carolina: D, 50.36%
Data Sources
- Popular Vote Data, national and by state, 1948–2020
- Electoral College Distribution, national, 1948–2024
- Demographics Data, by state
- Primary Turnout Data, national and by state, 1789–2020
- Polling Data, National & State, 1968–2024
- FRED Economic Data, national, 1927-2024
- ANES Data, national
- Voter File Data, by state