With the election finally concluded and all states accounted for, I now take on the task of evaluating my final and other weeks’ models to determine their accuracy and understand why the election outcome was so far from what I predicted.
While my final prediction had Harris winning by a healthy margin in the electoral college, as I return to my models post election I see that the result is not completely different from what I predicted. Almost every model I have every created had either candidate winning within the margin of error for almost every state. Though my final model was less conservative than my past weeks, as noted this was partially due to last minute changes I had to make in my ensembling and modeling approach. Overall, though my predictions overtime all chose Kamala Harris to win the presidency, a Trump win was in the margin of error, but as we will evaluate below a win by this much was unexpected given my model. I will evaluate how this could have happened and what steps I could take to improve on this below.
Review of Models and Predictions
In this section, I review the forecasting models developed throughout weeks 1 to 9 and the results each yielded. Each model was built with a unique combination of variables and assumptions, leading to varying results. By walking through the results and calculations from each week, I reflect on which model performed best and why. While most of these were not in my final prediction, we will look through each step in the week-by-week decision making process where assumptions or decisions may have led to overfitting, bias, and other contributors to my prediction’s differences. Some of these models were reviewed and updated with new data through week 6, making their predictions more timely.
Week 1: This week used a simplified Norpoth model to make a prediction based on a weighted average of the election results from 2016 and 2020 by state. The predictive model can be defined as \(vote_{2024} = 0.75vote_{2020} + 0.25vote_{2016}\). This forecast resulted in Harris 276 - Trump 262.
Week 2: This week focused on economic variables and linear regressions. Evaluating a variety of economic fundamentals as predictors of two way popular vote, I found Q2 GDP growth in the election year to be the best predictor by on R sqaured, RMSE, and a variety of other linear model evaluations as compared to other economic variables. This forecast focused on two way popular vote, leading to a result of Harris 51.585% - Trump 48.415%.
Week 3: The main two models developed this week were ensembled elastic net regression models that weighed fundamentals more closer to the election and weighed polling more closer to the election. The final forecast for this week was an unweighted average between the two, leading to Harris 52.25% - Trump 49.85% when updated with new polling data.
Week 4: During this week, I began to narrow my work only down to the seven critical states: Arizona, Georgia, Michigan, Nevada, North Carolina, Pennsylvania, and Wisconsin. The model used was a super-learning model, leading to Harris 287 - Trump 251. The predictors used were polling, economic fundamentals, and lagged vote share of 2016 and 2020 in a pooled model.
Week 5: In week 5, I used a linear regression model with the predictors lagged popular vote, latest poll average, mean poll average, a weighted average of turnout, GDP quarterly growth, and RDPI quarterly growth. The results of two separate models led to predictions that added to above 100% for the combined vote share of the two parties, which I handled by comparing the two. My goal in this case was to get at solely electoral college, but updated this with a binomial model will be explored below. This was once again a pooled model. The results led to an outcome of Harris 292 - Trump 246 in the updated simulations.
Week 6: This week maintained the same prediction from last week, but urged inclusion of FEC contributions data in future models to see if it improves fit. The prediction remained Harris 292 - Trump 246.
Week 7: This week evaluated the results of model sin weeks 1-6, similar to the above. It also introduced the binomial simulations model, which predicted turnout as a weighted average of linear and GAM predictions. The simulations drawing from the binomial distribution using polling averages and standard deviations as hyperparameters and size of draws of the voter eligible population predicted above, this resulted in Harris 270 - Trump 268. This was my closest prediction of any week, with the result in any of the battleground states being within the margin of error. The result of this year’s election was therefore contained within the prediction interval of this model.
Week 8: Making small tweaks to the binomial simulations model, I ended up with the same results as week 7, Harris 270 - Trump 268, with the results in all battleground states being within the margin of error. This week’s prediction therefore also captured the actual result.
Final Prediction: For my 2024 election prediction, I explored various models to project presidential race outcomes, ultimately deciding on a linear regression model to predict vote margins after initial technical issues with a logistic regression and binomial simulations approach. My final model draws on predictors like polling data, voter turnout, past vote shares, and economic indicators such as GDP and income growth interacted with incumbency. Simulation results showed close races in swing states, with Democratic victories projected in Wisconsin, Michigan, Nevada, Pennsylvania, Georgia, and North Carolina, while Arizona leaned Republican. Predictive intervals indicated significant uncertainty in the swing states, but my model ultimately suggested a likely Democratic win, forecasting 308 Electoral College votes for Harris and 230 for Trump. While data limitations prevented me from incorporating ensembling, this simplified linear model provides a moderate accuracy level, with promising projections for Democratic outcomes across swing states. The actual results of the election were captured within the predictive intervals for each swing state.
While none of these models provided the exact correct result, or even winner, of the election, their predictive intervals are quite large and often include the end result. However, evaluating their accuracy more closely and making observations about where they went wrong, including on important variables, performance of past elections versus today, and turnout, can be instructive for understanding how our democracy currently functions and what brought about the end result.
Examining specific areas where these models diverged from reality, such as underestimating or overestimating support in particular demographic groups, can highlight biases in the data or assumptions that may need to be recalibrrated in future predictions. For instance, variations in regional turnout or unexpected shifts in key swing states may reveal trends not captured by conventional data inputs, signaling areas for future improvement in turnout models, particularly post-COVID and 2016 with Trump’s rise which may not be well suited by using years before in prediction. Evaluating these discrepancies can be particularly enlightening, as it allows us to identify potential blind spots in the models and understand how emerging societal changes impact voter behavior. Additionally, this examination provides a window into the assumptions embedded in these models, which may reflect outdated understandings of the electorate that are less applicable in today’s dynamic political climate.
Analysis of 2024 County Level Results
Before quantitatively analyzing the accuracy of my models, I will review the results of the 2024 election. Many of the graphs below are courtesy of Matthew Dardet, the teaching fellow of this course.
First, looking at the states which each candidate won in the end, we see that our seven swing states– Wisconsin, Michigan, Arizona, Nevada, Georgia, and North Carolina– were all won by the Republicans. None of my previous predictions had this outcome as the point estimate outcome.
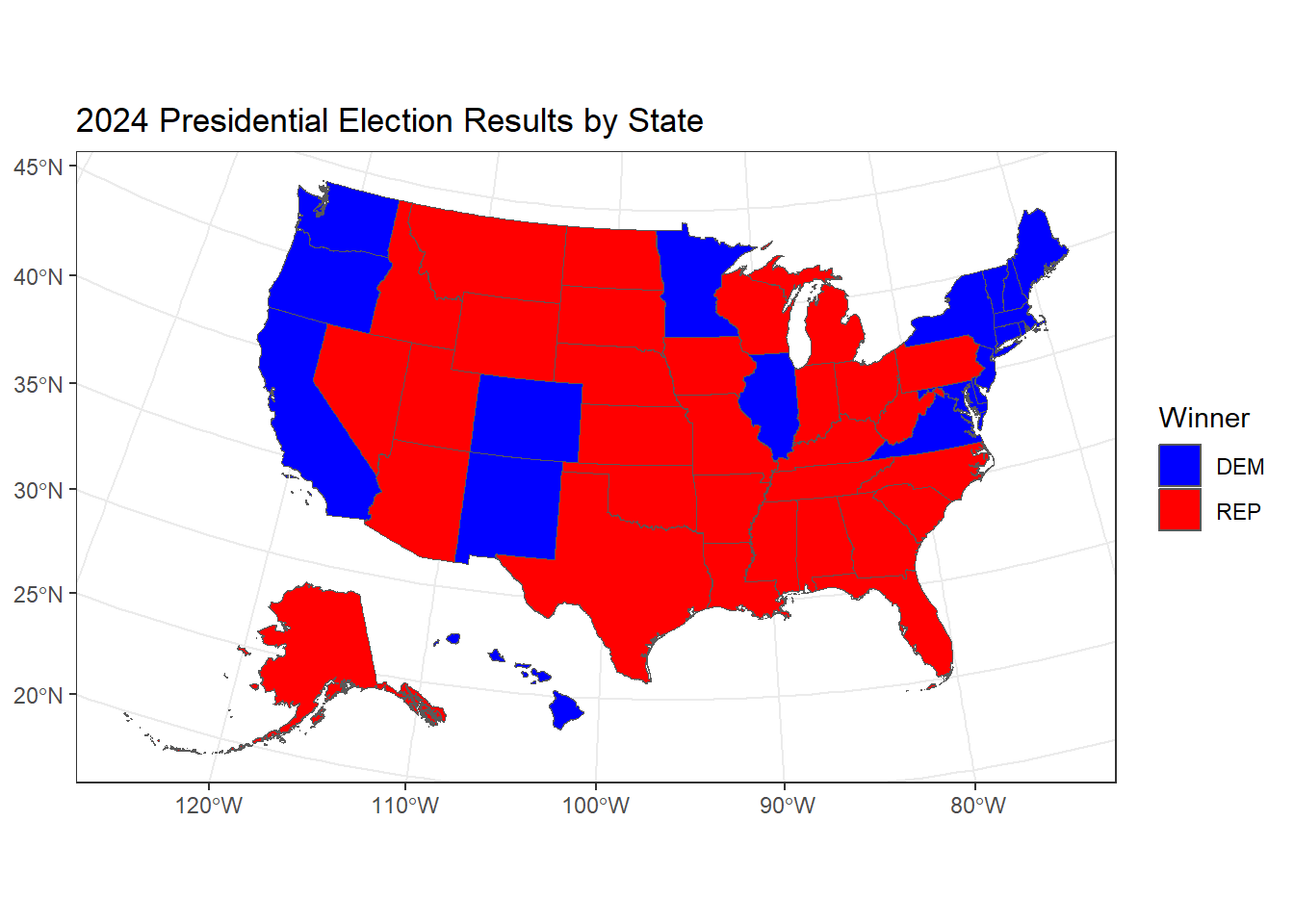
I can also look at how individual counties within these states shifted compared to 2020 election results. The average shift of a county, for those who data has been made available, is 1.885619 percentage points in the direction of the Republicans. This shift can be seen across the US, including in traditionally strong blue states which still went to Kamala Harris like California and New York. A map of these shifts across US states with data availabel can be seen below.

The patterns on the map above may be difficult to see, so I can also look individually at important swing states to see how they compare to the 2020 results. As a reminder, the results in 2020 were
- Arizona, 49.4% Biden
- Nevada, 50.1% Biden
- Pennsylvania, 50% Biden
- North Carolina, 49.9% Trump
- Georgia, 49.5% Biden
- Wisconsin, 49.4% Biden
- Michigan, 50.6% Biden
The changes for each swing state by county can be visualized below.
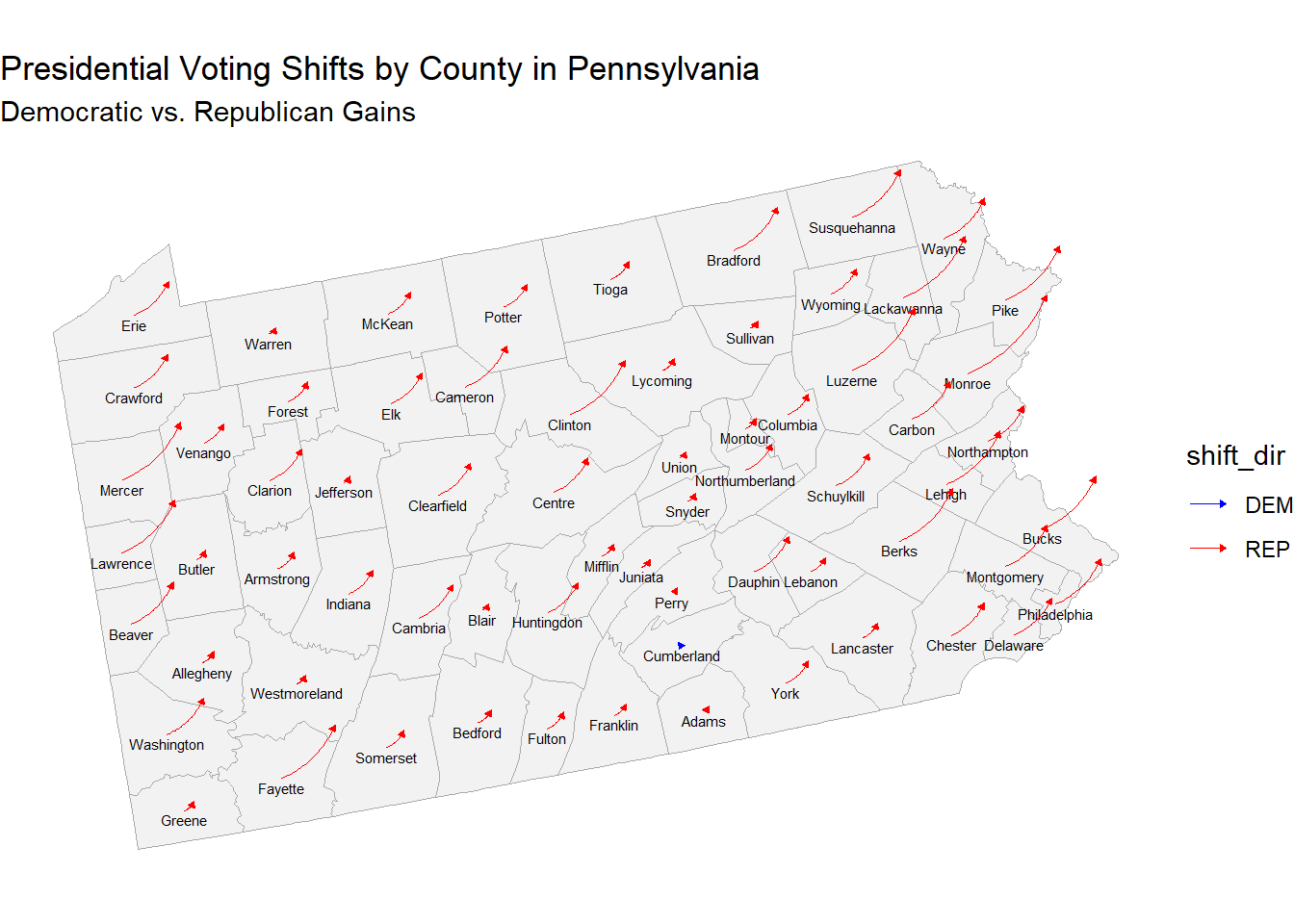
As seen across the country, counties in Pennsylvania shifted almost unanimously to the right with the popular vote amounts per county. In a state like Pennsylvania which was necessary in many Democratic strategies to 270, and a place that was the subject of a lot of campaigning and money by both campaigns, analyzing why this is the case may help explain the election result.
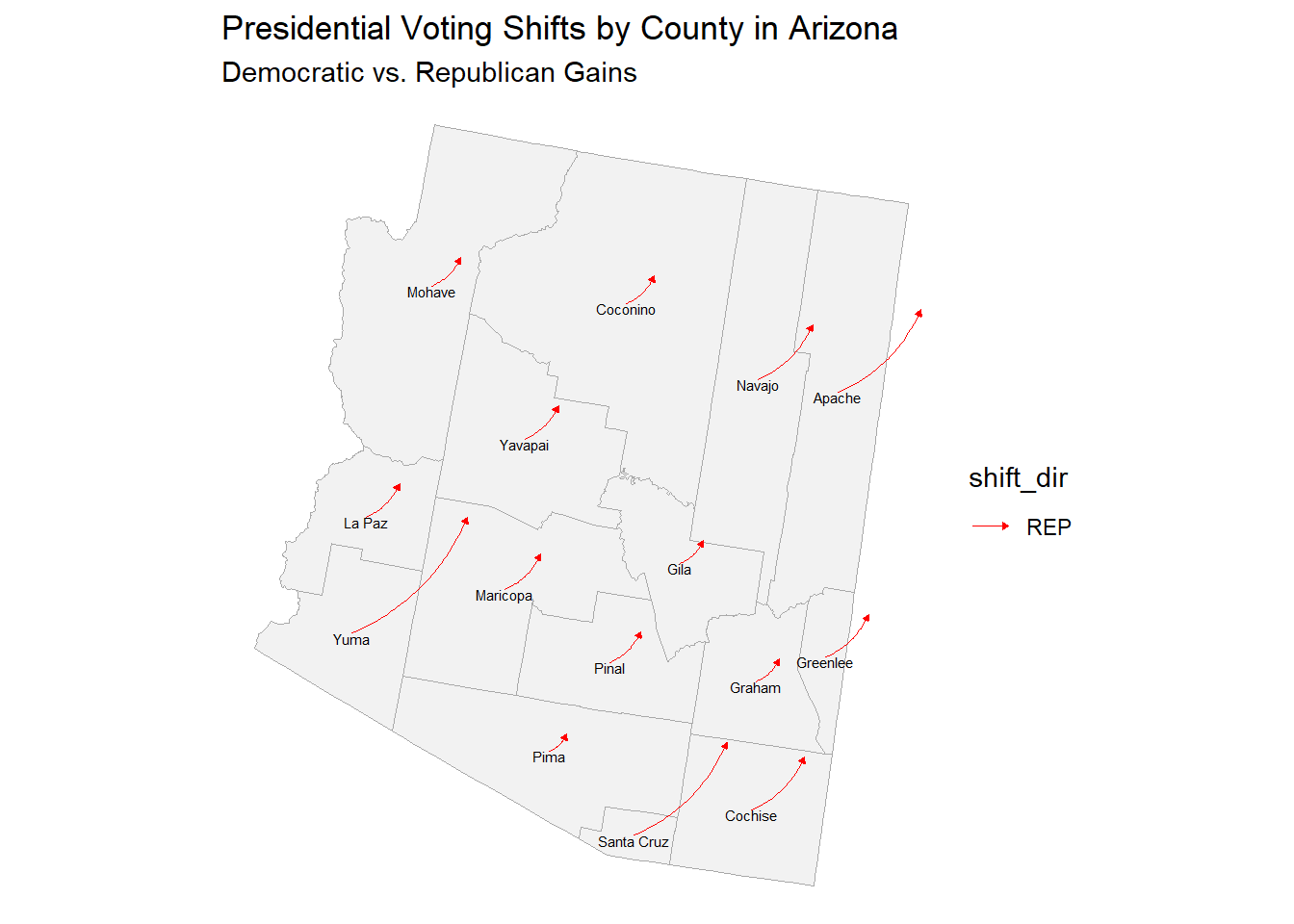
All Arizona counties had swing to the right, some with large amounts like in Yuma county which shifted by 10.6705605 percentage points towards Trump. Apache and Santa Cruz had similarly large shifts to the right compared to 2020. It is worth noting that both Yuma and Santa Cruz county are on the US-Mexico border.

Nevada had some small left and right shifts compared to 2020, but the large shifts were all in favor of the Republicans. Shifts to the Democrats were incredibly small in magnitude.
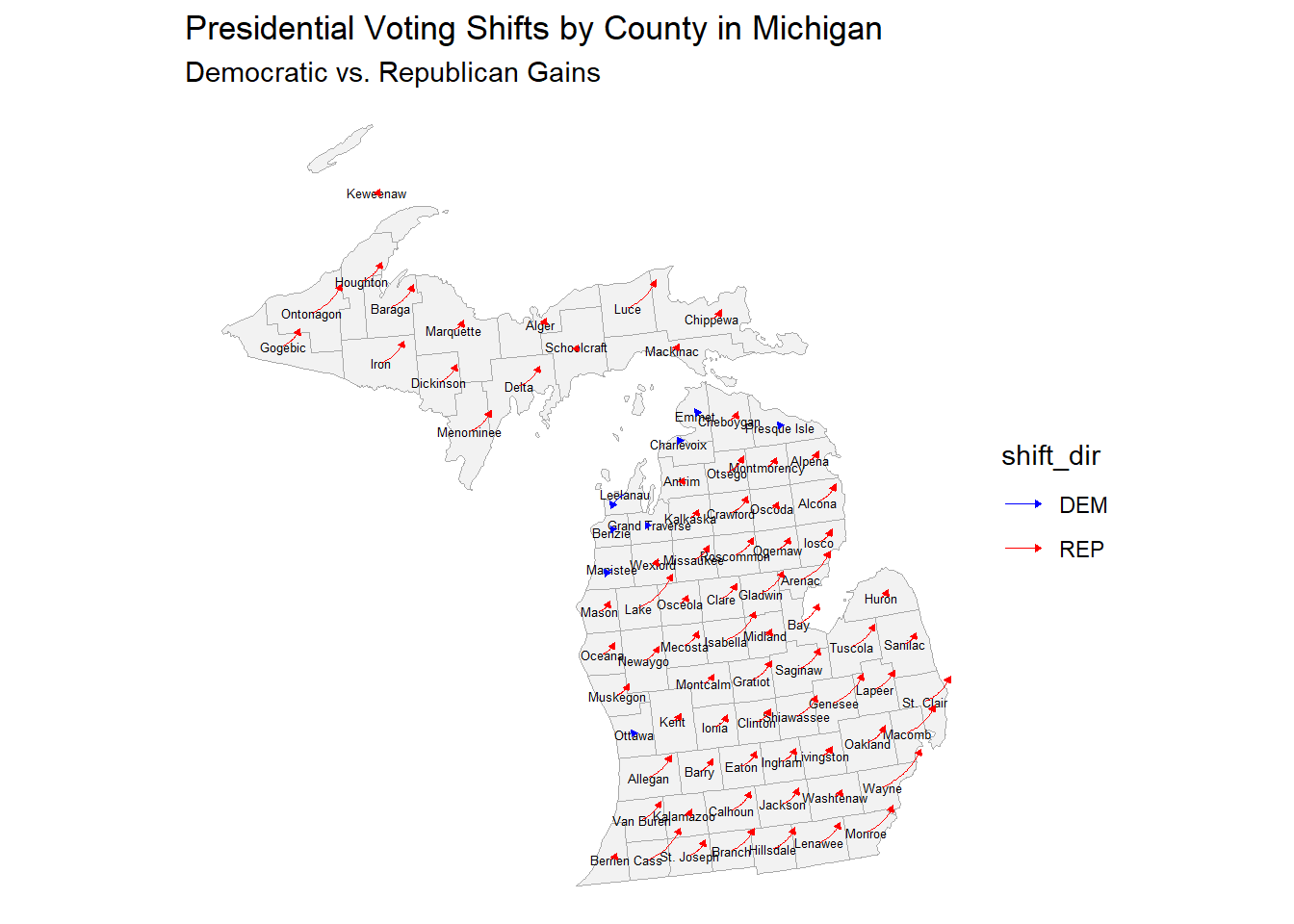
The is a pretty uniform right shift across Michigan counties in the lower peninsula. The upper peninsula had larger shifts towards Trump. There were also countries along the northwestern counties of Michigan which had small left shifts, but they were once again small in magnitude. Urban areas, not only in Michigan but across all states, had right shifts. Urban centers are traditionally a stronghold for Democrats. Though they may have still won many urban counties, the rightward shift leads to smaller margins which contribute to their loss on a statewide popular vote level.
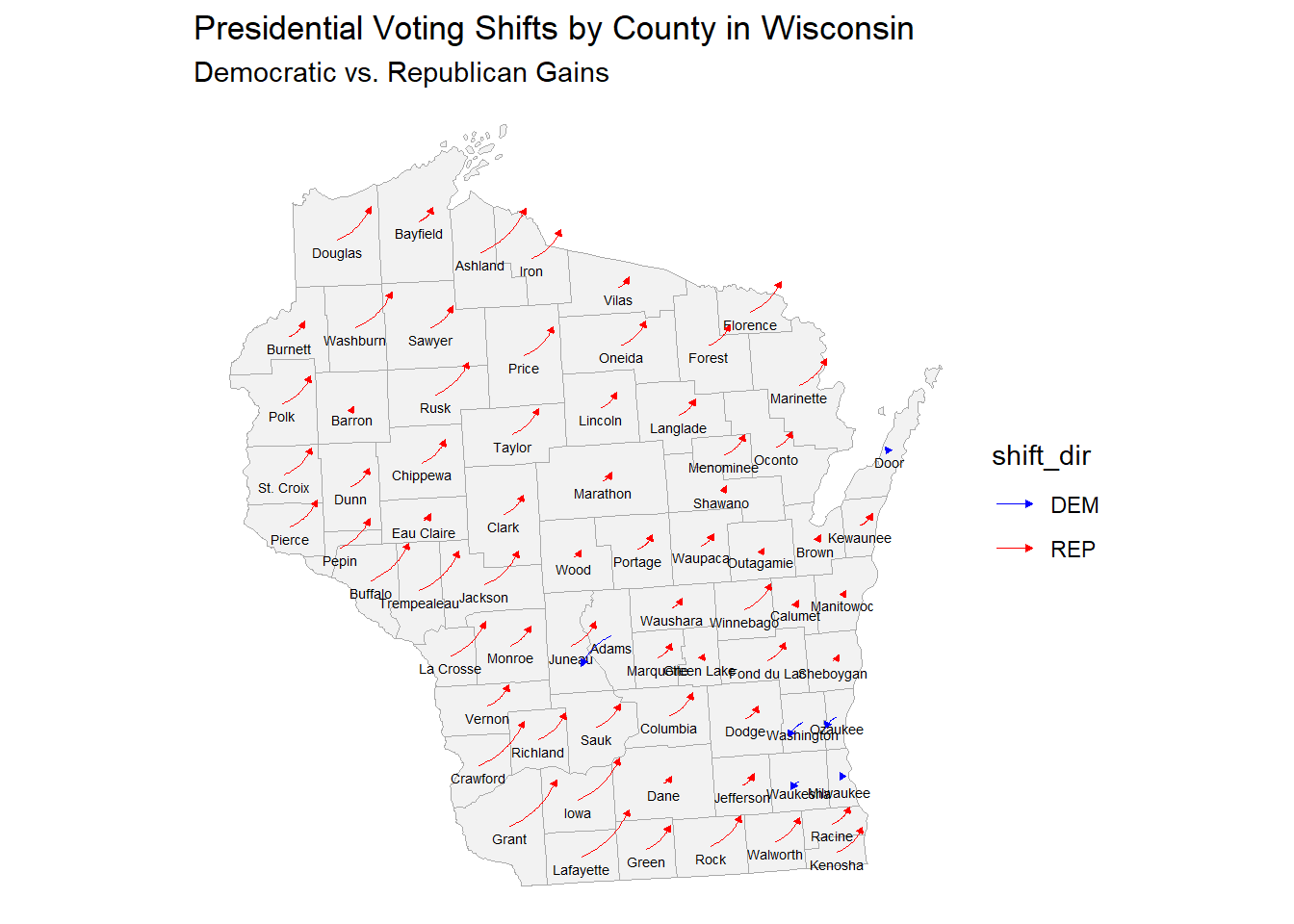
Like with Michigan, many counties had a moderately large rightward shift compared to 2020. Unlike other swing states, some countries had a slightly larger left shift as well, like Adams county in central Wisconsin. Urban areas like Milwaukee shifted left in Wisconsin, which is a contrast to other urban areas shifting right.
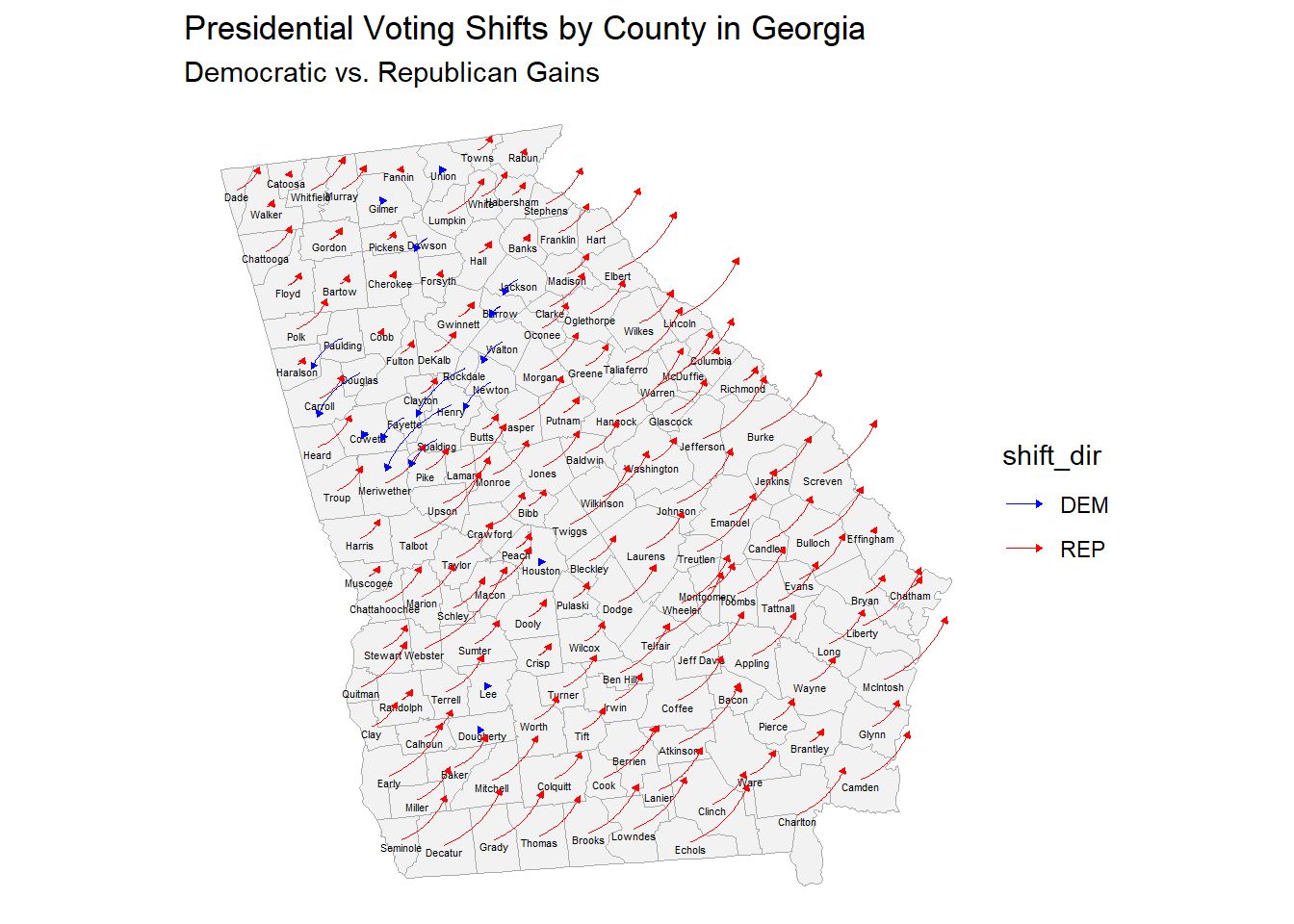
Again, many large shifts to the republicans occurred in Georgia, particularly rural counties. Around Atlanta, some suburban counties had significant blue shifts, but otherwise were overpowered by the across the board rightward shift.
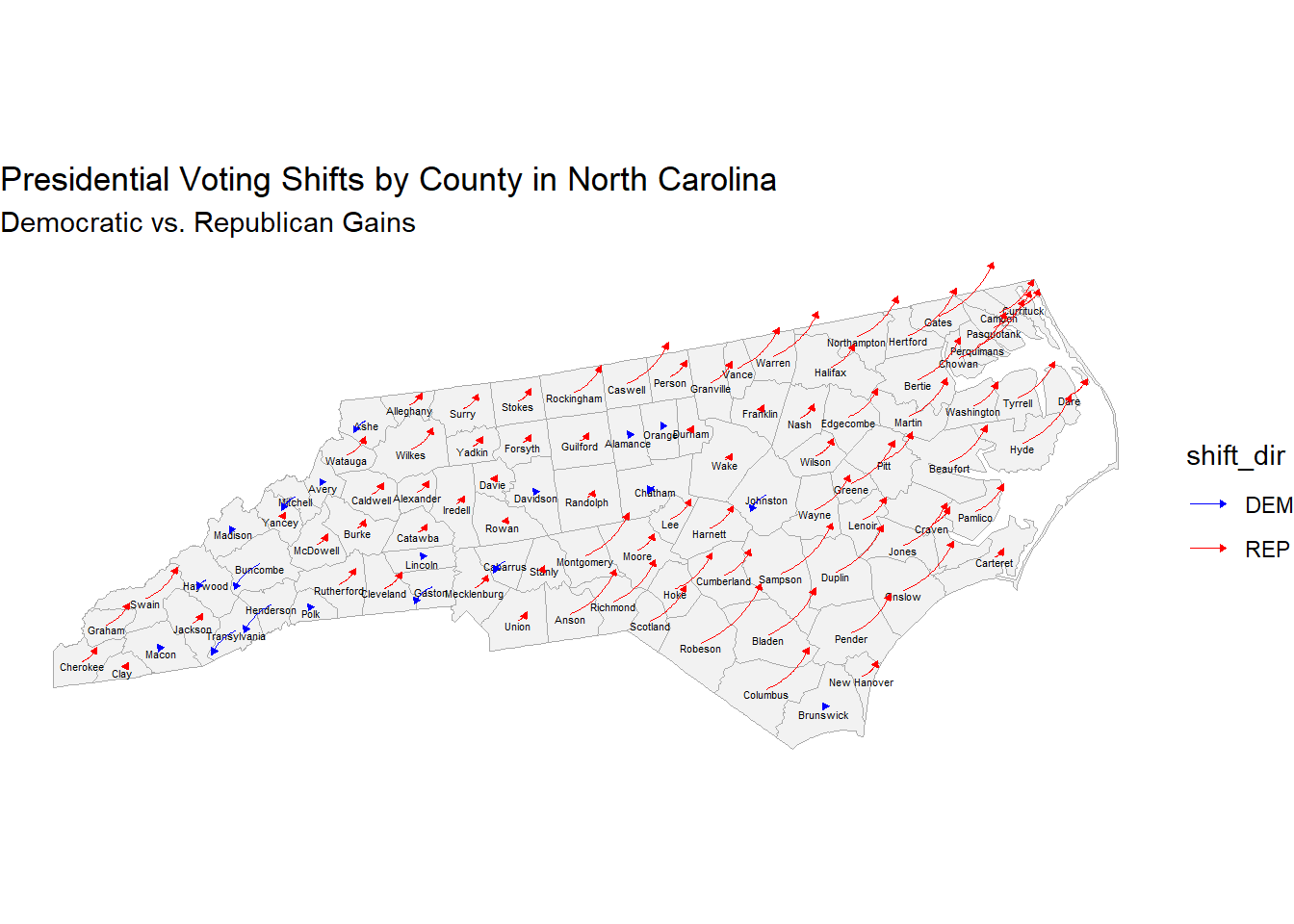
In North Carolina, the magnitude of rightward shifts is again much larger than leftward shifts, though there are more counties in this state compared to others with a blue shift in 2024. Many counties had large Republican shifts in support.
Overall, the 2024 results show a nearly uniform shift even at the county level of support for Trump in 2024 compared to 2020. We analyze the reasons for why this was not predicted by my models below.
Accuracy of the Final Model
Now I will begin to assess the accuracy of my final model. To do this, I will look at a variety of measures of accuracy including the MSE, RMSE, MAE, and bias. I will also look at confusion matrices for the simulations I ran and make an ROC curve of the results.
First, I examine the mean squared error for each the my predictions in the seven states of interest I predicted the popular vote outcomes from. This is found by calculating the average of the squares of the errors. I will calculate this on the democratic party two way popular vote values that I predicted and those that were observed.
## MSE: 4.373352## RMSE: 2.091256## MAE: 2.045356## Bias: 2.045356Looking at these results, we can interpret the error in our results. An MSE of 4.373352 means that, on average, the squared error between the two-party democratic popular vote share my model predicted and the actual outcome in vote share is about 4.37 percentage points squared. This value gives a sense of how large the errors tend to be, but the interpretation is abstract because it’s squared. Therefore, I look at the root mean squared error, or RMSE. An RMSE of 2.091256 means that, on average, my model’s predictions for the Democratic two-party vote share are off by about 2.09 percentage points. RMSE of 2.09 percentage points is a relatively small error in the context where vote shares typically range from 40% to 60%, so an error of 2 percentage points means my model’s predictions are reasonably close to the actual outcomes. However, this only moderate amount of error still led my overall outcome to be wildly different from the actual outcome, given that those two points determined the difference between the winner and loser in every swing state.
Mean absolute error (MAE) measures the average of the absolute differences between predicted and actual vote share values. An MAE of 2.05 percentage points means that, on average, my model’s predicted two-party vote share is off by about 2.05 percentage points from the actual vote share in 2024. Like RMSE, MAE reflects the average prediction error, but unlike MSE and RMSE, it does not give more weight to larger errors. The MAE is not significantly different from the RMSE, indicating that there are not very many large errors. The bias and MAE give the same result because the model is consistently making errors of the same sign, under-predicting the results for the Republicans and over-predicting for the Democrats.
Across all four of these error calculations, my model’s predictions for the Democratic two-party vote share were generally close, with average errors around 2 percentage points, although they led to a different result for all of the states due to how close the values were to 50%.
For think linear regression model, which was described above, I also ran simulations. I can make confusion matrices for the predictions made by the 10000 simulations run using the model of each state by varying turnout. It may have been more effective to vary polling numbers to carry out simulations, as noted in the final prediction, which will be even more important when discussing polling bias as a source of error in my model in the following section. The confusion matrices for the predictions in each state are shown below.
| Republican | Democrat | |
|---|---|---|
| Republican | 23 | 0 |
| Democrat | 9977 | 0 |
| Republican | Democrat | |
|---|---|---|
| Republican | 0 | 0 |
| Democrat | 10000 | 0 |
| Republican | Democrat | |
|---|---|---|
| Republican | 1 | 0 |
| Democrat | 9999 | 0 |
| Republican | Democrat | |
|---|---|---|
| Republican | 7861 | 0 |
| Democrat | 2139 | 0 |
| Republican | Democrat | |
|---|---|---|
| Republican | 1855 | 0 |
| Democrat | 8145 | 0 |
| Republican | Democrat | |
|---|---|---|
| Republican | 2044 | 0 |
| Democrat | 7956 | 0 |
| Republican | Democrat | |
|---|---|---|
| Republican | 4826 | 0 |
| Democrat | 5174 | 0 |
As expected, in the states where the model predicted the majority of the cases to be democratic wins, as occurred in Michigan, Pennsylvania, and Wisconsin, the confusion matrices will result in very low accuracy. However, in the other states, the accuracy is higher, with the highest accuracy being in Arizona with 78.61%. It is worth noting that in states like Michigan, Pennsylvania, and Wisconsin, my accuracy with this final model was near 0%. This is different when looking at my binomial simulations model, which I will also analyze below.
Accuracy of the Binomial Simulations Model
I will also look briefly at the binomial simulations model. This was not my final model due to issues in the final stages, so the version solely using polling– which was leftwardly biased in this election as discussed below– is included for analysis. I first rerun the binomial simulations model for each of the seven swing states below.
I start with the outcomes for Wisconsin, then each of the other swing states
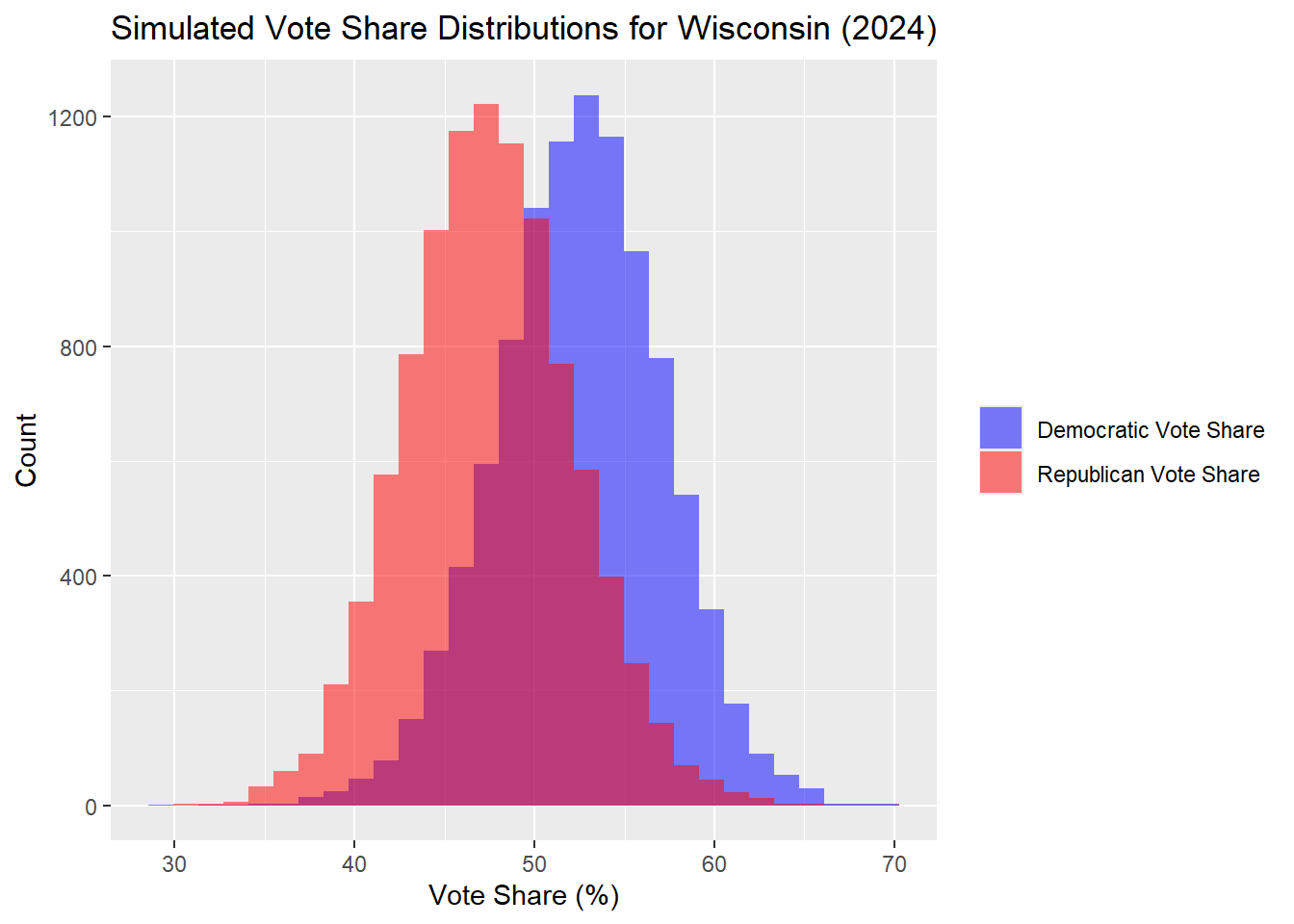
## The median Democrat two-way popular vote predicted is: 52.6## The median Republican two-way popular vote predicted is: 47.4| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -16.51 |
| 50% | Median | -5.19 |
| 90% | 90th Percentile | 6.81 |
Now below are the results for Nevada.
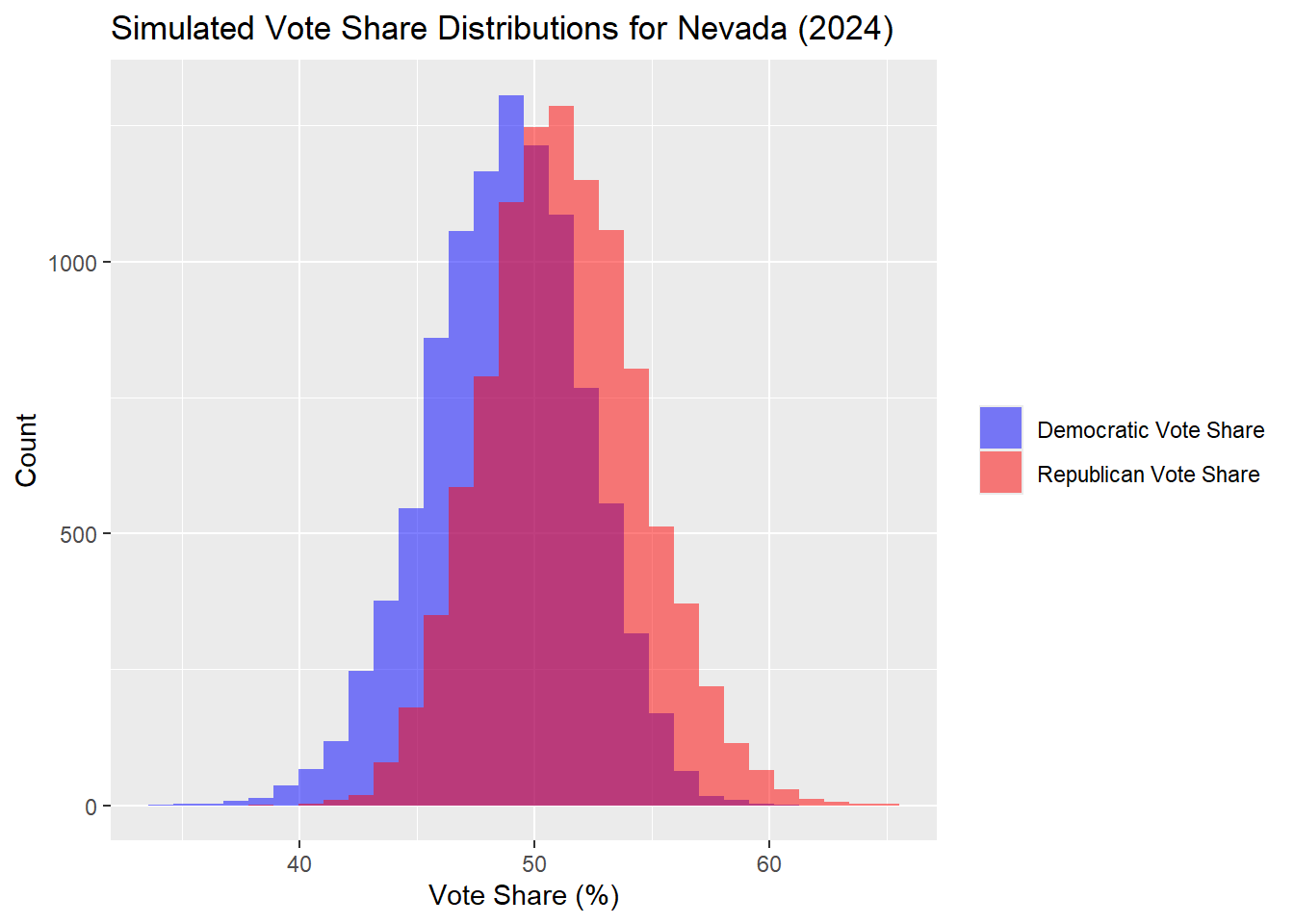
## The median Democrat two-way popular vote predicted is: 48.89## The median Republican two-way popular vote predicted is: 51.11| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -5.94 |
| 50% | Median | 2.23 |
| 90% | 90th Percentile | 10.94 |
Arizona results are below.
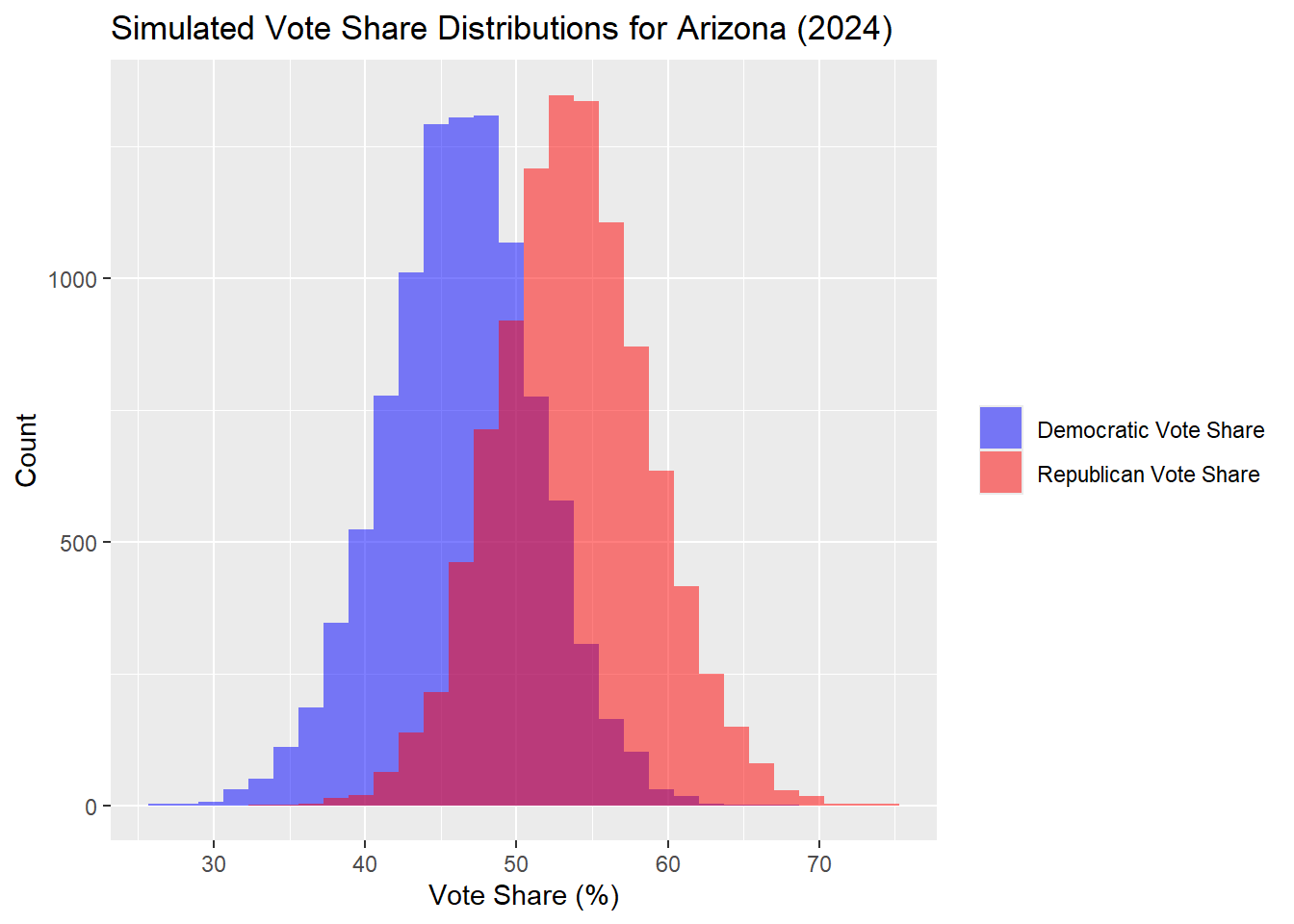
## The median Democrat two-way popular vote predicted is: 46.36## The median Republican two-way popular vote predicted is: 53.64| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -5.20 |
| 50% | Median | 7.29 |
| 90% | 90th Percentile | 20.43 |
Now I calculate this for North Carolina.
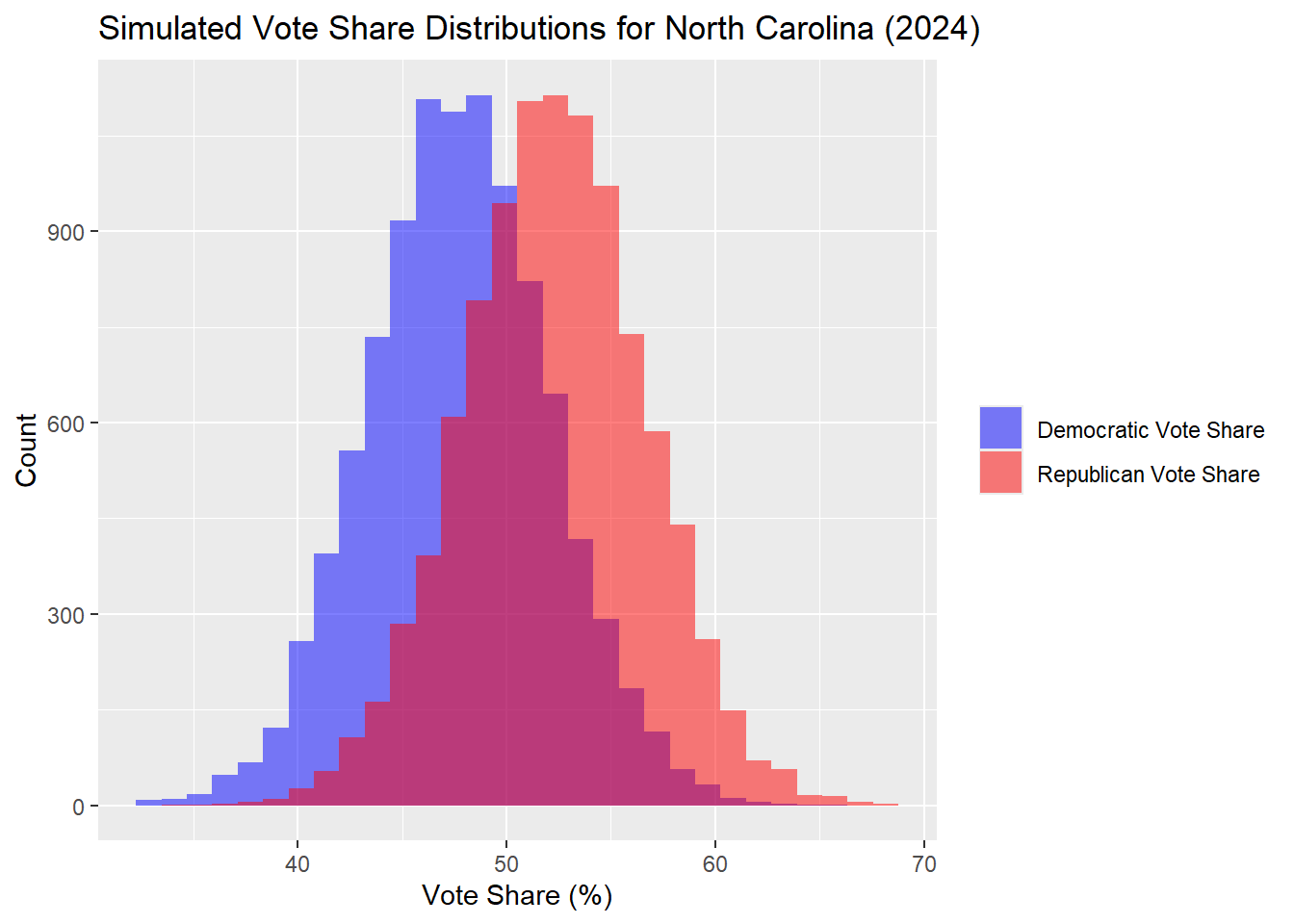
## The median Democrat two-way popular vote predicted is: 47.73## The median Republican two-way popular vote predicted is: 52.27| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -6.49 |
| 50% | Median | 4.53 |
| 90% | 90th Percentile | 15.66 |
And this is calculated for Georgia.
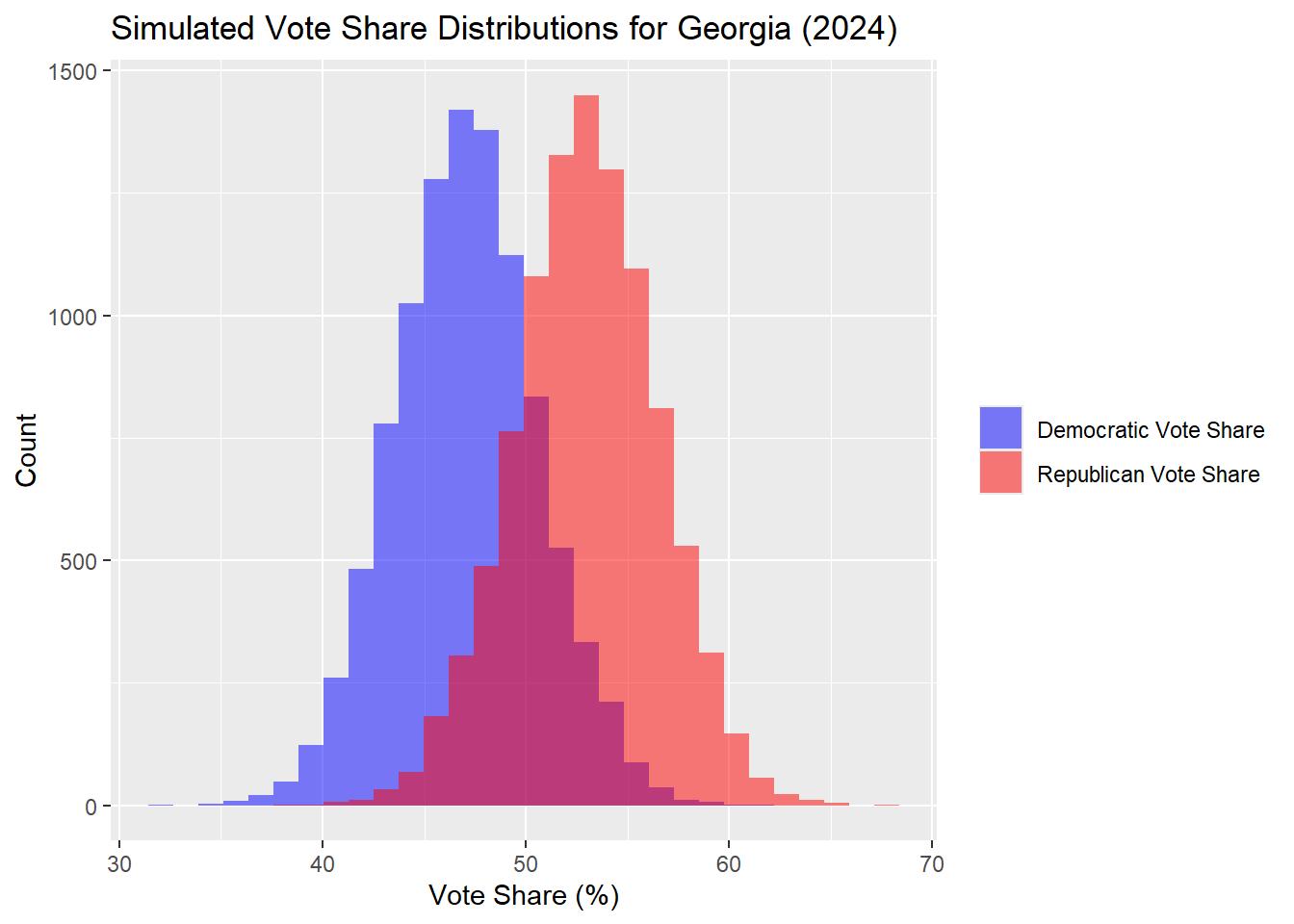
## The median Democrat two-way popular vote predicted is: 47## The median Republican two-way popular vote predicted is: 53| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -3.08 |
| 50% | Median | 6.00 |
| 90% | 90th Percentile | 14.81 |
Next, for Michigan.
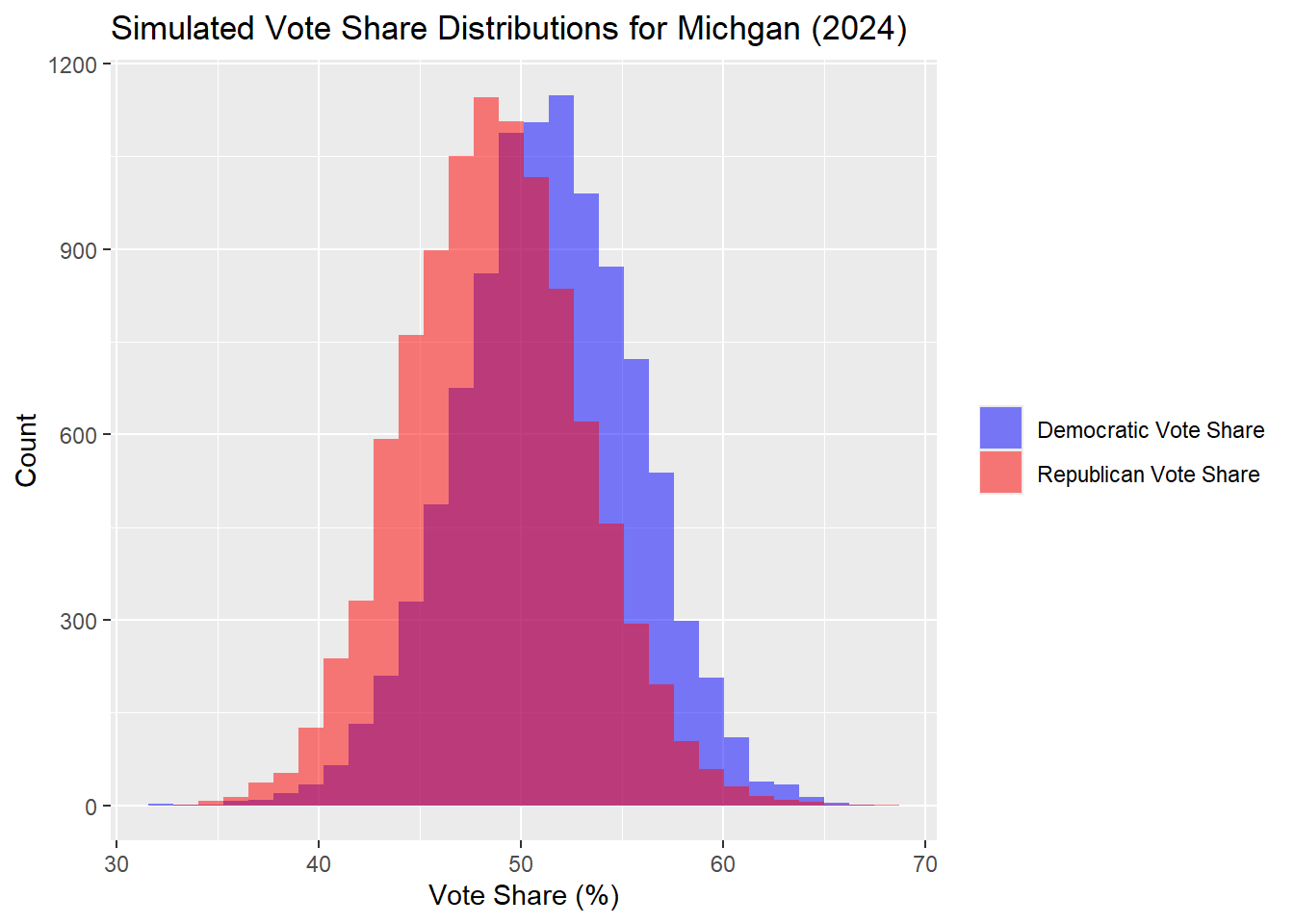
## The median Democrat two-way popular vote predicted is: 51.35## The median Republican two-way popular vote predicted is: 48.65| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -13.68 |
| 50% | Median | -2.70 |
| 90% | 90th Percentile | 8.61 |
And finally, for Pennsylvania.
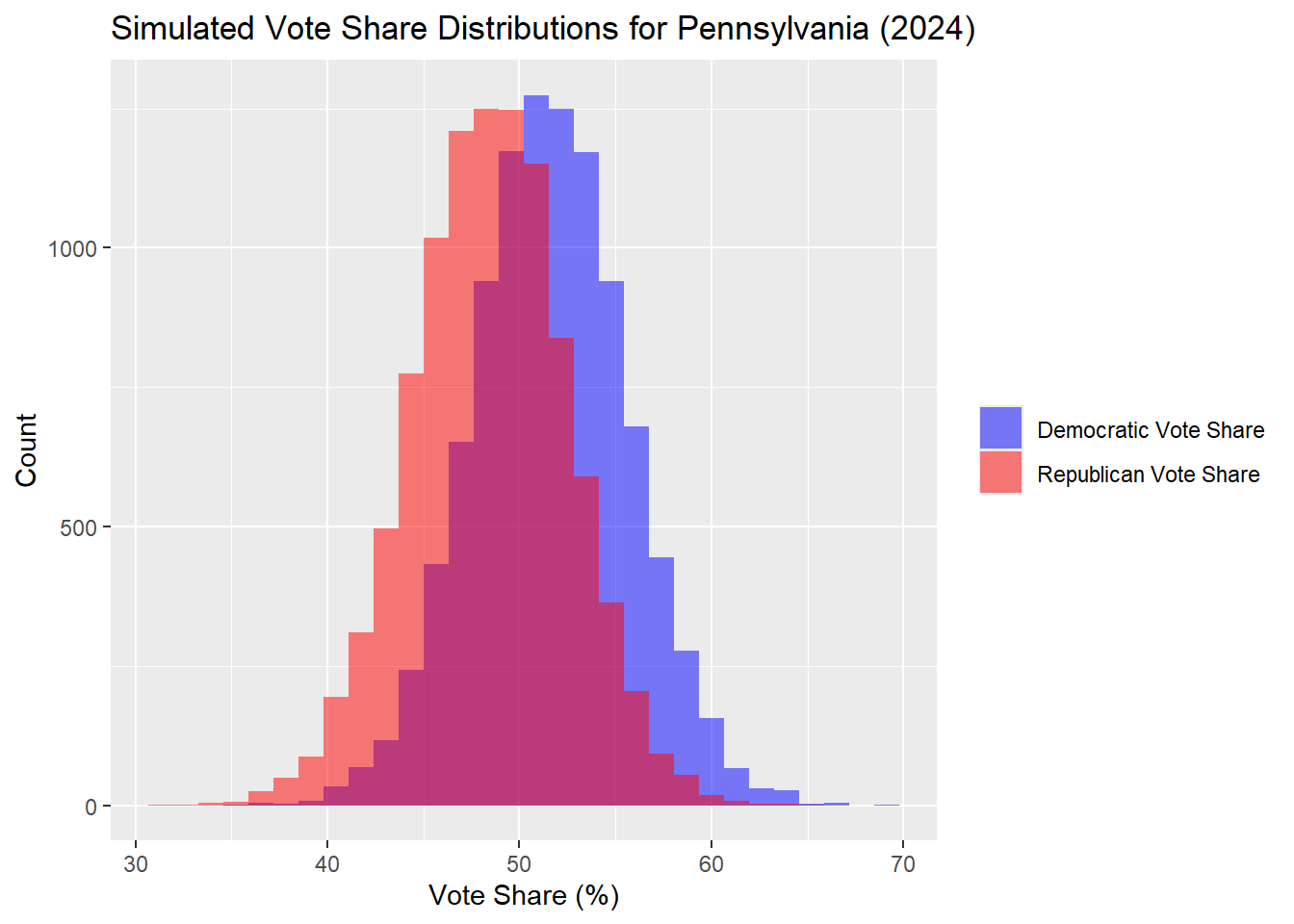
## The median Democrat two-way popular vote predicted is: 51.56## The median Republican two-way popular vote predicted is: 48.44| Percentile | Margin (R - D) | |
|---|---|---|
| 10% | 10th Percentile | -13.51 |
| 50% | Median | -3.12 |
| 90% | 90th Percentile | 7.02 |
In this model, the result was that Harris won Pennsylvania, Michigan, and Wisconsin. This is the 270 Harris - 268 Trump result that was predicted before. I can evaluate the accuracy of this prediction with the same measures as above, allowing me also to compare the two models. On the surface level, the electoral college outcome is closer to the actual outcome.
## MSE: 2.598515## RMSE: 1.611991## MAE: 1.39615## Bias: 0.3159973The model’s performance metrics indicate that its predictions of Democratic two-party vote shares are relatively accurate. The MSE of 2.65 suggests that the average squared difference between predicted and actual vote shares is small, reflecting minimal deviation from the actual result. Similarly, the RMSE of 1.63 percentage points quantifies this deviation on a comparable scale to the original data, such that there is on average 1.63 percentage point deviation from the actual result. This is not bad overall, but in context the predicted values are so close to 50% that this deviation can change the result of a state or even the whole election. Additionally, the MAE of 1.41 percentage points highlights that the typical prediction error is just about one and a half percentage points. These results suggest that the model provides predictions that are useful for understanding Democratic vote share, but they are still closer to 50% overall, making the predictions off from the actual result.
The bias metric further reveals a slight systematic over-prediction in the model. With a positive bias, the model tends to estimate Democratic vote shares marginally higher than the actual values. While this overestimation is small, in a close election where even a fraction of a percentage point could influence strategic decisions, it can lead to incorrect predictions. Recognizing and accounting for this bias could improve the predictions, as I will try to account for below.
Learning from 2020
After the 2020 election, Alan Abramowitz, the creator of the time for change model, wrote an article for the Center for Politics: Sabato’s Crystal Ball on how to evaluate the forecasts of 2020 post-election. Abramowitz notes how important the assumptions that political scientists decided to implement in their models were, especially due to the 2020 election being during COVID. Though 2024 was not a COVID year, I would argue these changes are still ongoing, brought on not only by COVID but also larger structural changes in American democracy and the opinions of the people, still complicating the forecasting process. While in aggregate forecasting models in 2020 were accurate, individual models were not and varied a lot.
For 2020, Abramowitz notes that incorpating economic conditions which would usually reflect on the incumbent would have inaccurately used the effect of COVID, which many did not blame on the current President Trump, to his disadvantage. The same blame effect for the economy could be affecting my model here, as the current economic conditions may not be tied directly to Vice President Harris, and more so she may be effected by the negatives in the economy than the positives given her position, though empirically this is unknown.
Abramowitz also discusses how early polling in the primaries may have been an inaccurate predictor. This is also a useful discussion in 2024 given the candidate switch. Understanding how the polls affect Harris, especially incorporating them pre-candidate switch, and how they may have been inflated due to the recency of the candidate switch and wave of movement and action it caused only among the already most enagaged democrats may be worth exploring. Taking unusual circumstances into account, with a former president against a candidate-switch candidate, may be worth exploring how to integrate into future models, if they are quantifiable.
Understanding the Inaccuracies
Moving beyond a direct analysis of the inaccuracies of my model, I move to make theoretically testable hypotheses to understand which locations and assumptions within my model contributed to the incorrect result. As noted above, the end result was in the margin of error for many if not all of my prior weeks models, but because the confidence intervals were so large this is unsurprising. Instead, I will focus on why the point estimate of the result may have been inaccurate, shying away from solely pointing to the quality of my model inputs and instead focusing on why certain components may not have have been predictive.
Arguments for why models like mine were inaccurate should not fall simply to bad data inputs, though critically analyzing these inputs is important. In fact, 538 early analysis found that polling data were actually the lowest in error as they have been in the past 25 years, but instead may have had bias in the direction of Harris. This bias was lower than in 2016 and 2020 polling, but higher than the years prior to that. 538’s takeaway well summed it up: “Pollsters are having a hard time reaching the types of people who support Trump.” However, this is not the only reason I believe my model was incorrect, as I believe there are issues with the model assumptions above and beyond the quality of its components.
One such potential reason why the components of my model may not have been predictive in the same way as they are in the training set of past elections could be the connection between Harris as the current Vice President and the economy. Though Harris is not technically the incumbent president, she was coded as such in my model, following the idea that the quarter two growth in the year of the election reflects either well or poorly on the current president and will affect their vote share. However, in this case, it is not clear if the same relationship between incumbency and economic indicators holds, making the weight placed on incumbency difficult to determine. I weighted my model such that Harris was treated as the full incumbent, therefore having the full effect of the economic interaction variables with incumbency trained on actual incumbents of the past. It is likely that the relationship between a sitting vice president and how much they are tied to the economic outcomes of their administration are slightly different, though it is unclear if they would have more or less of a magnitude of an effect, and as such this interaction variable may have been less predictive than its performance in past elections. Economic indicators have always had a large place in even the simplest models like the time for change model, so a differing level of predictiveness of them due to the unique circumstances of this election could have thrown off my prediction.
More potential differences between my model and the outcome also arise out of the candidate switch. The candidate switch from Joe Biden to Kamala Harris for the democrats in July may have motivated active democrats even more than they already were against Trump. The switch also could realign the base of the democrats to a group that is more engaged under a Harris candidacy than Biden, but whom are not the traditional base and therefore are not taken into account in turnout models. It is worth noting that Harris, as the first woman of color to receive a major party’s presidential nomination, might resonate more strongly with demographic groups that Biden didn’t energize as effectively, such as younger voters, women, and people of color. This increased enthusiasm could drive higher turnout among these groups, especially in swing states, which a static model may not capture. However, the model may not also capture changes in predicted turnout through which Harris either pushed democrats away from voting for her or away from voting at all. My turnout model did not account for a shift the Democratic base itself. Furthermore, Harris’s presence on the ticket might intensify opposition among Republicans. As a more progressive figure, she could encourage higher turnout from conservative voters who may have been less motivated by Biden. My prediction and turnout models relied on historical data, but this kind of candidate switch is unprecedented, which limits the model’s ability to make accurate predictions based on past outcomes alone even with interventions in weighting.
Testing My Hypothesis
To test my hypotheses and ideas related to the inaccuracies in my model, I will propose quantitative tests to evaluate whether the assumptions made in the model were accurate or whether changes in the political and economic landscape led to deviations from past patterns.
One test I could do would test the economic fundamentals and their effect on Harris’s vote share. My model assumed that economic indicators, which are traditionally linked to an incumbent president’s electoral success, would also apply to Harris in her role as vice president. However, this relationship may not hold, as her association with economic outcomes may differ from that of a sitting president. To test this, I could conduct a study in a counterfactual world where Biden did not drop out and there was a non-Trump and therefore non-former president other candidate, such that testing the combinations of Harris, Biden, Trump, and not Trump would allow me to see how economic fundamentals, such as GDP growth and RDPI growth, affected democratic vote share in each place. I would also look at swing states relative to non-swing states. This would help determine whether the same economic relationship holds for a vice president as it does for a president.
Another potential source of inaccuracy is the candidate switch from Biden to Harris in 2024, which may have led to inflated polling numbers or shifts in voter turnout that were not captured in my model. A time-series analysis could be employed to examine polling data before and after the candidate switch, assessing whether there was a significant spike in support for Harris among specific demographics or regions that could be controlled for. Additionally, a difference-in-differences approach could compare voter turnout in states with significant candidate-switch effects seen in polling versus those that didn’t have a change. These tests would help determine whether the model failed to capture changes in voter behavior driven by Harris’s candidacy.
The bias in polling data could also be a contributing factor to the model’s inaccuracy. According to 538’s post-election analysis, polling data may have overstated Harris’s support, especially among certain demographic groups. To test this hypothesis, I could compare polling data with actual voting outcomes, particularly in key swing states, to determine if specific groups were overrepresented in pre-election polls and adjust my turnout model to handle this.
Lastly, Harris’s candidacy may have intensified opposition among Republicans, driving higher conservative turnout. A regression could analyze changes in Republican turnout from 2020 to 2024, controlling for party loyalty, candidate preferences, and demographic shifts. This would help determine whether Harris’s presence on the ticket had a distinct impact on conservative voter engagement, particularly in swing states.
By conducting these quantitative tests, I would be able to better understand the sources of inaccuracy in my model and determine whether unique factors like the candidate switch and shifting voter behaviors contributed to the deviations from historical trends. Testing the effects of economic conditions, polling biases, and changes in Republican base engagement would help refine future models by accounting for these variables, ultimately improving the accuracy of predictions in future elections.
If I Could Do It All Over
As discussed in last week’s post, the binomial model with variables in addition to polling I had planned to use met a sudden end. My original plan was to combine the presented linear model, an elastic net model, and the binomial model through super learning to get rid of the potential biases inherent in each formulation while using the same predictors, something I don’t usually see in ensembling. This allows the model to balance the benefits of pooled predictions with the more specific insights from multiple models.
Additionally, I would rely less on polling and more on economic fundamentals. I would also work more to understand the way to manage incumbency in my model with these economic fundamentals. In addition to these, I would make the changes described in the understanding the inaccuracies section. Overall, I would work more on building out the binomial simulations model and focusing more on economic variables.
Data Sources
- Popular Vote Data, national and by state, 1948–2020
- Electoral College Distribution, national, 1948–2024
- Demographics Data, by state
- Primary Turnout Data, national and by state, 1789–2020
- Polling Data, National & State, 1968–2024
- FRED Economic Data, national, 1927-2024
- ANES Data, national
- Voter File Data, by state
- 2024 Returns by County and State
Thank you for following along this semester. JS.